题目内容

19．若△ABC的三个内角满足tanAtanBtanC＞0，则△ABC是（　　）
A．锐角三角形B．直角三角形C．钝角三角形D．任意三角形

分析 由已知不等式，利用正切函数的单调性确定出A，B，C的范围，即可作出判断．

解答 解：∵△ABC的三个内角满足tanAtanBtanC＞0，
∴tanA＞0，tanB＞0，tanC＞0，
∴A，B，C都为锐角，
则△ABC为锐角三角形，
故选：A．

点评 此题考查了三角形形状的判断，熟练掌握正切函数的单调性是解本题的关键．

练习册系列答案
相关题目
9．对于函数f（x）=xex有以下命题：
①函数f（x）只有一个零点； 
②函数f（x）最小值为-e； 
③函数f（x）没有最大值； 
④函数f（x）在区间（-∞，0）上单调递减．
其中正确的命题是（只填序号）①③．
10．一个几何体的三视图如图所示，则这个几何体是（　　）
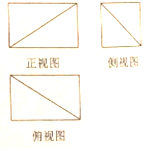
A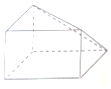．B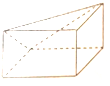．C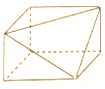．D．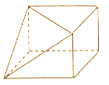
7．i是虚数单位，若复数z满足zi=-1+i，则复数z的共轭复数是（　　）
A．1-iB．1+iC．-1+iD．-1-i
14．已知函数f（x）=ex-ax有两个不同的零点，
（Ⅰ） 求实数a的取值范围．
（Ⅱ）设f（x）的极值点为x=x0，证明：对任意的x＞0，恒有不等式f（x0+x）＞f（x0-x）成立．
4．设正项等比数列{an}的前n项和为Sn，且满足S3=3a3+2a2，a4=8．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设数列bn=log2an，求{|bn|}的前n项和Tn．
11．圆x2+（y-1）2=4上点到曲线f（x）=-x3+3x2在点（1，f（1））处的切线的最远距离为（　　）
A．$\frac{\sqrt{10}}{4}$B．$\frac{10+\sqrt{10}}{5}$C．$\frac{10-\sqrt{10}}{5}$D．$\frac{10+2\sqrt{10}}{5}$
8．设$\overrightarrow{a}$=2（sinx，1-$\sqrt{2}$cosx），$\overrightarrow{b}$=（cosx，1+$\sqrt{2}$cosx），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$（x∈R）．
（1）求函数f（x）的解析式；
（2）求函数f（x）的最小正周期，当x∈[-$\frac{3}{8}$π，$\frac{3}{8}$π]时，求f（x）的单调增区间．
9．计算log25•log32•log53的值为（　　）
A．1B．2C．4D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网