题目内容
一名箭手进行射箭训练,箭手连续射2支箭,已知射手每只箭射中10环的概率是
,射中9环的概率是
,射中8环的概率是
,假设每次射箭结果互相独立.
(1)求该射手两次射中的总环数为18环的概率;
(2)设该箭手两次射中的总环数为ζ,求ζ的分布列和数学期望.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
(1)求该射手两次射中的总环数为18环的概率;
(2)设该箭手两次射中的总环数为ζ,求ζ的分布列和数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(1)由题意知运动员两次射击是相互独立的,根据相互独立事件同时发生的概率,得到该运动员两次都命中18环的概率.
(2)该运动员两次射击中最高环数作为他的成绩记为ξ,确定ξ的可能取值,结合变量对应的事件,写出变量的概率,写出分布列和期望.
(2)该运动员两次射击中最高环数作为他的成绩记为ξ,确定ξ的可能取值,结合变量对应的事件,写出变量的概率,写出分布列和期望.
解答:
解:(1)由题意知箭手两次射击是相互独立的,
根据相互独立事件同时发生的概率得到该射手两次射中的总环数为18环的概率为
+
•
=
;
(2)ξ的可能取值为20、18、16、19、17
P(ξ=20)=
;P(ξ=18)=
;P(ξ=16)=
;P(ξ=19)=
;P(ξ=17)=
∴ξ的分布列为
∴ξ的数学期望为Eξ=20×
+18×
+16×
+19×
+17×
=
.
根据相互独立事件同时发生的概率得到该射手两次射中的总环数为18环的概率为
| 1 |
| 16 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 16 |
(2)ξ的可能取值为20、18、16、19、17
P(ξ=20)=
| 1 |
| 16 |
| 3 |
| 16 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
∴ξ的分布列为
| ξ | 20 | 18 | 16 | 19 | 17 | ||||||||||
| P |
|
|
|
|
|
| 1 |
| 16 |
| 3 |
| 16 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 8 |
| 191 |
| 16 |
点评:本题考查离散型随机变量的分布列和期望,考查相互独立事件同时发生的概率,是一个综合题,这类问题的解法实际上不困难,只要注意解题的步骤就可以.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
如图:四面体P-ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为( ) 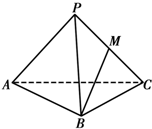

A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
 如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC=
如图,梯形BCDE中,DE∥BC,CD⊥DE,ED=DC= 如图,已知:平行四边形ABCD是矩形,AB=2,BC=1.PD⊥平面ABCD,且PD=3.
如图,已知:平行四边形ABCD是矩形,AB=2,BC=1.PD⊥平面ABCD,且PD=3.