题目内容
已知|
|=|
|=λ|
+
|,且实数λ∈[
,1],则
与
-
的夹角取值范围是 .
| a |
| b |
| a |
| b |
| ||
| 3 |
| b |
| a |
| b |
考点:数量积表示两个向量的夹角
专题:平面向量及应用
分析:如图所示,以OA,OB为邻边作平行四边形,且
=
,
=
,设<
,
>=θ.在△OAC中,由余弦定理可得cos(π-θ)=1-
.再利用实数λ∈[
,1],即可得出θ的取值范围,进而得出答案.
| OA |
| a |
| OB |
| b |
| a |
| b |
| 1 |
| 2λ2 |
| ||
| 3 |
解答:
解:如图所示,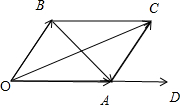
以OA,OB为邻边作平行四边形,且
=
,
=
,设<
,
>=θ.
∵|
|=|
|=λ|
+
|,
∴在△OAC中,由余弦定理可得cos(π-θ)=
=
=1-
.
∴cosθ=
-1.
∵实数λ∈[
,1],
∴(
-1)∈[-
,
].
∴θ∈[
,
].
当θ=
时,∠OBA=∠BAC=
∠OAC=
(π-
)=
,∴
与
-
的夹角=π-
=
.
当θ=
时,∠OBA=∠BAC=
∠OAC=
(π-
)=
,∴
与
-
的夹角=π-
=
.
∴
与
-
的夹角取值范围是[
,
].
故答案为:[
,
].

以OA,OB为邻边作平行四边形,且
| OA |
| a |
| OB |
| b |
| a |
| b |
∵|
| a |
| b |
| a |
| b |
∴在△OAC中,由余弦定理可得cos(π-θ)=
|
| ||||||
2|
|
2|
| ||||||
2|
|
| 1 |
| 2λ2 |
∴cosθ=
| 1 |
| 2λ2 |
∵实数λ∈[
| ||
| 3 |
∴(
| 1 |
| 2λ2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴θ∈[
| π |
| 3 |
| 2π |
| 3 |
当θ=
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| b |
| a |
| b |
| π |
| 3 |
| 2π |
| 3 |
当θ=
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
| π |
| 6 |
| b |
| a |
| b |
| π |
| 6 |
| 5π |
| 6 |
∴
| b |
| a |
| b |
| 2π |
| 3 |
| 5π |
| 6 |
故答案为:[
| 2π |
| 3 |
| 5π |
| 6 |
点评:本题考查了向量的平行四边形法则、余弦定理、向量的夹角等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设n∈N+,曲线y=xn在x=2处的切线与y轴交点的纵坐标为an,则a3为( )
| A、-3 | B、-8 |
| C、-16 | D、-24 |
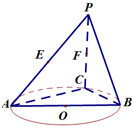 如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.