题目内容
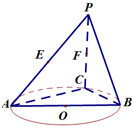 如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.(Ⅰ)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明.
(Ⅱ)设(Ⅰ)中的直线l与圆O的另一个交点为D,记直线DF与平面ABC所成的角为θ,直线DF与直线BD所成的角为α,二面角E-BD-C的大小为β,求证:sinθ=sinαsinβ.
考点:与二面角有关的立体几何综合题,空间中直线与平面之间的位置关系
专题:空间角
分析:(I)由已知条件推导出EF∥AC,从而得到EF∥平面ABC,由此能证明l∥平面PAC.
(II)过B作AC的平行线BD,交线l即为直线BD,且l∥AC,由已知条件推导出∠CBF=β,∠CDF=θ,∠BDF=α,由此能证明sinθ=sinαsinβ.
(II)过B作AC的平行线BD,交线l即为直线BD,且l∥AC,由已知条件推导出∠CBF=β,∠CDF=θ,∠BDF=α,由此能证明sinθ=sinαsinβ.
解答:
(I)解:∵E,F分别是PA,PC的中点,
∴EF∥AC,∵AC?平面ABC,EF不包含于平面ABC,
∴EF∥平面ABC.
又∵EF?平面BEF,平面BEF∩平面ABC=l
∴EF∥l,∴l∥平面PAC.…(4分)
 (II)证明:如图,过B作AC的平行线BD,
(II)证明:如图,过B作AC的平行线BD,
由(I)知,交线l即为直线BD,且l∥AC.
∵AB是⊙O的直径,∴AC⊥BC,于是BD⊥BC.
∵PC⊥平面ABC,∴PC⊥BD,
∴BD⊥平面PBC.连接BE,BF,则BD⊥BF.
∴∠CBF就是二面角E-BD-C的平面角,即∠CBF=β.…(7分)
连结CD,∵PC⊥平面ABC,∴CD就是FD在平面ABC内的射影,
∴∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又∵BD⊥平面PBC,∴BD⊥BF,则∠BDF为锐角,∠BDF=α.…(9分)
∴在Rt△CDF,Rt△BDF,Rt△BCF中,分别得
sinθ=
,sinα=
,sinβ=
,
∴sinαsinβ=
•
=
=sinθ,
∴sinθ=sinαsinβ.…(12分)
∴EF∥AC,∵AC?平面ABC,EF不包含于平面ABC,
∴EF∥平面ABC.
又∵EF?平面BEF,平面BEF∩平面ABC=l
∴EF∥l,∴l∥平面PAC.…(4分)
 (II)证明:如图,过B作AC的平行线BD,
(II)证明:如图,过B作AC的平行线BD,由(I)知,交线l即为直线BD,且l∥AC.
∵AB是⊙O的直径,∴AC⊥BC,于是BD⊥BC.
∵PC⊥平面ABC,∴PC⊥BD,
∴BD⊥平面PBC.连接BE,BF,则BD⊥BF.
∴∠CBF就是二面角E-BD-C的平面角,即∠CBF=β.…(7分)
连结CD,∵PC⊥平面ABC,∴CD就是FD在平面ABC内的射影,
∴∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又∵BD⊥平面PBC,∴BD⊥BF,则∠BDF为锐角,∠BDF=α.…(9分)
∴在Rt△CDF,Rt△BDF,Rt△BCF中,分别得
sinθ=
| CF |
| DF |
| BF |
| DF |
| CF |
| BF |
∴sinαsinβ=
| BF |
| DF |
| CF |
| BF |
| CF |
| DF |
∴sinθ=sinαsinβ.…(12分)
点评:本题考查直线与平面的位置关系的判断与证明,考查三角函数正弦值相等的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(
如图,在菱形ABCD中,AB=BD=2,三角形PAD为等边三角形.将它沿AD折成大小为α(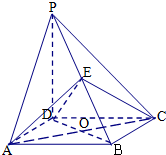 如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.
如图四棱锥P-ABCD中,底面ABCD是正方形,PD⊥底面ABCD,点E在棱PB上.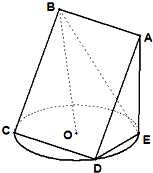 如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3
如图,正方形ABCD所在平面与圆O所在平面相交于CD,线段CD为圆O的弦,AE垂直于圆O所在平面,垂足E是圆O上异于C、D的点,AE=3,正方形的边长为3