题目内容
若双曲线
-
=1的一条渐近线方程为x+3y=0，则此双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由双曲线
-
=1的一条渐近线方程为x+3y=0，可得
=
，即可求出双曲线的离心率．
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| 1 |
| 3 |
解答：
解：∵双曲线
-
=1的一条渐近线方程为x+3y=0，
∴
=
，
∴e=
=
，
故选：B．
| x2 |
| a2 |
| y2 |
| b2 |
∴
| b |
| a |
| 1 |
| 3 |
∴e=
| ||
| a |
| ||
| 3 |
故选：B．
点评：本题考查双曲线的性质，考查学生的计算能力，属于基础题．
练习册系列答案
金博士一点全通系列答案
相关题目
已知α为锐角，cos（α+
）=
，则sinα=（ ）
| π |
| 6 |
| 2 |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
函数y=tanx+
是（ ）
| 1 |
| tanx |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
已知向量
=（-2，1），向量
与
的夹角为180°，且|
|=2
，则
=（ ）
| β |
| α |
| β |
| α |
| 5 |
| α |
| A、（-4，2） |
| B、（4，-2） |
| C、（-4，-2） |
| D、（4，2） |
在[0，2π]上满足cos（
-α）≥
的α取值范围是（ ）
| 5π |
| 2 |
| 1 |
| 2 |
A、[0，
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
如图是一个算法的流程图．若输入x的值为2，则输出y的值是（ ）
| A、0 | ||
B、-
| ||
| C、-1 | ||
D、-
|
过曲线y=
x3上的点P的切线l的方程为12x-3y=16，那么P点坐标可能为（ ）
| 1 |
| 3 |
A、（1，-
| ||
B、（2，
| ||
C、（-1，-
| ||
D、（3，
|
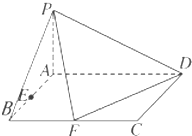已知四棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，AD=2，AB=1，E，F分别是线段AB，BC的中点，