题目内容
如图是一个算法的流程图.若输入x的值为2,则输出y的值是( )


| A、0 | ||
B、-
| ||
| C、-1 | ||
D、-
|
考点:程序框图
专题:算法和程序框图
分析:根据框图的流程依次计算程序运行的结果,直到满足条件|y-x|<1,跳出循环体,计算输出y的值.
解答:
解:由框图的流程知:输入x=2,第一次循环y=
×2-1=0,|y-x|=2>1;
第二次循环x=0,y=
×0-1=1,|y-x|=1;
第三次循环x=1,y=
×1-1=-
,|y-x|=
>1;
第四次循环x=-
,y=
×(-
)-1=-
,|y-x|=
<1,满足条件|y-x|<1,跳出循环体,
输出y=-
.
故选:D.
| 1 |
| 2 |
第二次循环x=0,y=
| 1 |
| 2 |
第三次循环x=1,y=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
第四次循环x=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 3 |
| 4 |
输出y=-
| 5 |
| 4 |
故选:D.
点评:本题考查了循环结构的程序框图,根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法.

练习册系列答案
相关题目
已知向量
=(3,1),
=(1,3),
=(k,7),若(
-
)∥
,则k=( )
| a |
| b |
| c |
| a |
| c |
| b |
| A、1 | B、3 | C、5 | D、7 |
若双曲线
-
=1的一条渐近线方程为x+3y=0,则此双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
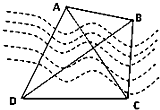 如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )
如图,A、B两点都在河的对岸(不可到达),为了测量A、B两点间的距离,选取一条基线CD,A、B、C、D在一平面内.测得:CD=200m,∠ADB=∠ACB=30°,∠CBD=60°,则AB=( )A、
| ||||
B、200
| ||||
C、100
| ||||
| D、数据不够,无法计算 |
在△ABC中,角A,B,C所对的边分别为a,b,c,若c=2asinC,则角A为( )
| A、30°或60° |
| B、45°或60° |
| C、120°或60° |
| D、30°或150° |
如果执行如图的程序框图,输出的S=72,则判断框中为( )


| A、k≥9 | B、k≤8 |
| C、k≤9 | D、k≥8 |
设等比数列{an}的前n项和为Sn,且S2=1,S4=3,则S6=( )
| A、5 | B、7 | C、9 | D、11 |