题目内容
某产品生产成本C万元与产量q件(q∈N*)的函数关系式为C=100+4q,销售单价p万元与产量q件的函数关系式为p=25-
q.当产量为多少件时,每件产品的平均利润最大,且最大值为多少?
| 1 |
| 4 |
考点:导数在最大值、最小值问题中的应用
专题:应用题,导数的综合应用
分析:求出销售收入、利润,可得每件产品的平均利润,利用导数即可求得最大值及产量q值.
解答:
解:销售收入R=q×p=25q-
q2,利润L=R-C=-
q2+21q-100,
每件产品的平均利润f(q)=
=21-(
q+
)(0<q<100且q∈N*)…(6分)
所以f/(q)=-
+
…(8分),解f′(q)=0得q=-20(舍去),或q=20…(9分),
当0<q<20时,f′(q)>0,f(q)单调递增;
当20<q<100时,f′(q)<0,f(q)单调递减…(11分).
所以产量q=20时,f(q)max=11…(13分)
| 1 |
| 4 |
| 1 |
| 4 |
每件产品的平均利润f(q)=
| L |
| q |
| 1 |
| 4 |
| 100 |
| q |
所以f/(q)=-
| 1 |
| 4 |
| 100 |
| q2 |
当0<q<20时,f′(q)>0,f(q)单调递增;
当20<q<100时,f′(q)<0,f(q)单调递减…(11分).
所以产量q=20时,f(q)max=11…(13分)
点评:本题考查应用导数求实际背景下函数的最值问题、二次函数的性质,考查学生应用数学知识解决实际问题的能力.

练习册系列答案
相关题目
若l,m为空间两条不同的直线,α,β为空间两个不同的平面,则l丄α的一个充分条件是( )
| A、l∥β且α丄β |
| B、l?β且α丄β |
| C、l丄β且α∥β |
| D、l丄m且m∥α |
对于定义在R上的奇函数f(x),满足f(x+3)=f(x),则f(1)+f(2)+f(3)=( )
| A、0 | B、-1 | C、3 | D、2 |
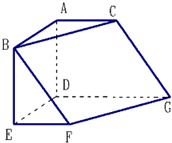 在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.
在图的几何体中,面ABC∥面DEFG,∠BAC=∠EDG=120°,四边形 ABED 是矩形,四边形ADGC 是直角梯形,∠ADG=90°,四边形 DEFG 是梯形,EF∥DG,AB=AC=AD=EF=1,DG=2.