题目内容
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |
考点:简单随机抽样,用样本的频率分布估计总体分布
专题:概率与统计
分析:根据总体、个体、样本、样本容量的定义,得出结论.
解答:
解:从某班50名学生中抽取6名学生进行视力状况的统计分析,
则50个学生的视力状况是总体,抽取的6名学生的视力是一个样本,
每个被调查的学生的视力状况是个体,样本容量是6,
结合所给的选项,只有C正确,
故选:C.
则50个学生的视力状况是总体,抽取的6名学生的视力是一个样本,
每个被调查的学生的视力状况是个体,样本容量是6,
结合所给的选项,只有C正确,
故选:C.
点评:本题主要考查总体、个体、样本、样本容量的定义,用样本频率估计总体分布,属于基础题.

练习册系列答案
相关题目
直线l:y=kx+4-2k与曲线y=1+
有两个交点时,实数k的取值范围是( )
| 4-x2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知直线l1:ax+(a+1)y+1=0,l2:x+ay+2=0,若l1⊥l2,则a=( )
| A、0 | B、-2 |
| C、0或-2 | D、0或2 |
二次方程ax2+bx+c=0的两根为-2,3,a<0,那么ax2+bx+c>0的解集为( )
| A、{x|x>3或x<-2} |
| B、{x|x>2或x<-3} |
| C、{x|-2<x<3} |
| D、{x|-3<x<2} |
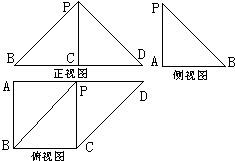 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( )
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边BD长为2;侧视图为一直角三角形;俯视图为一直角梯形,且AB=BC=1,则此几何体的体积是( ) 选修4-1:几何证明选讲
选修4-1:几何证明选讲