题目内容
直线l:y=kx+4-2k与曲线y=1+
有两个交点时,实数k的取值范围是( )
| 4-x2 |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
考点:直线与圆的位置关系
专题:直线与圆
分析:根据直线过定点,以及直线和圆的位置关系即可得到结论.利用数形结合作出图象进行研究即可.
解答:
解:由y=k(x-2)+4知直线l过定点(2,4),将y=1+
,两边平方得x2+(y-1)2=4,
则曲线是以(0,1)为圆心,2为半径,且位于直线y=1上方的半圆.
当直线l过点(-2,1)时,直线l与曲线有两个不同的交点,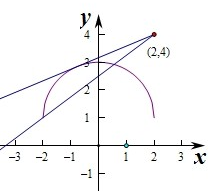
此时1=-2k+4-2k,
解得k=
,
当直线l与曲线相切时,直线和圆有一个交点,
圆心(0,1)到直线kx-y+4-2k=0的距离d=
=2,
解得k=
,
要使直线l:y=kx+4-2k与曲线y=1+
有两个交点时,
则直线l夹在两条直线之间,
因此
<k≤
,
故选:D.
| 4-x2 |
则曲线是以(0,1)为圆心,2为半径,且位于直线y=1上方的半圆.
当直线l过点(-2,1)时,直线l与曲线有两个不同的交点,

此时1=-2k+4-2k,
解得k=
| 3 |
| 4 |
当直线l与曲线相切时,直线和圆有一个交点,
圆心(0,1)到直线kx-y+4-2k=0的距离d=
| |3-2k| | ||
|
解得k=
| 5 |
| 12 |
要使直线l:y=kx+4-2k与曲线y=1+
| 4-x2 |
则直线l夹在两条直线之间,
因此
| 5 |
| 12 |
| 3 |
| 4 |
故选:D.
点评:本题主要考查直线和圆的位置关系的应用,利用数形结合是解决本题的关键,考查学生的计算能力.

练习册系列答案
 能力评价系列答案
能力评价系列答案
相关题目
不等式2x2+mx+n>0的解集是{x|x>3或x<-2},则二次函数y=2x2+mx+n的表达式是( )
| A、y=2x2+2x+12 |
| B、y=2x2-2x+12 |
| C、y=2x2+2x-12 |
| D、y=2x2-2x-12 |
若16-x2≥0,则( )
| A、0≤x≤4 |
| B、-4≤x≤0 |
| C、-4≤x≤4 |
| D、x≤-4或x≥4 |
已知直线y=x+b与曲线x2+y2=1(x>0)有交点,则( )
| A、-1<b<1 | ||||
B、-1<b<
| ||||
C、-
| ||||
D、-
|
方程ax2+2x+1=0恰有一个负实根,则a的取值范围为( )
| A、a<0 | B、a≤0 |
| C、a>0 | D、a=0 |
已知f(x)是定义在R上的偶函数,且对任意x∈R,总有f(x+2)=-f(x)成立,则f(19)=( )
| A、-2 | B、-1 | C、0 | D、19 |
从某班50名学生中抽取6名学生进行视力状况的统计分析,下列说法正确的是( )
| A、50名学生是总体 |
| B、每个被调查的学生是个体 |
| C、抽取的6名学生的视力是一个样本 |
| D、抽取的6名学生的视力是样本容量 |