题目内容
k取什么实数时，关于x的方程（k-2）x2-2x+1=0．
（1）有两个不相等的实根；
（2）有一个实根；
（3）没有实根．
（1）有两个不相等的实根；
（2）有一个实根；
（3）没有实根．
考点：一元二次方程的根的分布与系数的关系
专题：函数的性质及应用
分析：由条件利用判别式，求出k取什么实数时，关于x的方程（1）有两个不相等的实根；（2）有一个实根；（3）没有实根．
解答：
解：关于x的方程（k-2）x2-2x+1=0，
（1）当判别式△=4-4（k-2）=12-4k＞0时，即k＜3时，有两个不等的实数根．
（2）当△=4-4（k-2）=12-4k=0时，即k=3时，只有一个实数根．
（3）△=4-4（k-2）=12-4k＜0时，即k＞3时，没有实数根．
（1）当判别式△=4-4（k-2）=12-4k＞0时，即k＜3时，有两个不等的实数根．
（2）当△=4-4（k-2）=12-4k=0时，即k=3时，只有一个实数根．
（3）△=4-4（k-2）=12-4k＜0时，即k＞3时，没有实数根．
点评：本题主要考查一元二次方程根的分布与系数的关系，二次函数的性质，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
下列函数中，在其定义域内既是奇函数又是增函数的是（ ）
| A、y=x2 | ||
B、y=-
| ||
| C、y=x3 | ||
| D、y=log2x |
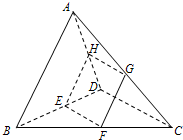三棱锥A-BCD中，面ACD与面BCD均为正三角形，点E，F，G，H分别为BD，BC，AC，AD中点