题目内容
已知函数y=f(x),我们把满足f(x0)=kx0的实数x0叫做函数f(x)的k倍不动点,设f(x)=x2+(2a+1)x+a2+a.
(1)若f(x)在区间[0,2]有两个相异的1倍不动点,求实数a,并求出此不动点;
(2)若对任意k≥3,f(x)都有k倍不动点,求实数a的取值范围;
(3)设m,n(m<n)为f(x)的2倍不动点,且函数f(x)在x∈[m,n]时值域为[2m,2n],求a的取值范围;
(4)函数f(x)在x∈[m,n](m<n)时单调,且值域恰为[2m,2n],求a的取值范围.
(1)若f(x)在区间[0,2]有两个相异的1倍不动点,求实数a,并求出此不动点;
(2)若对任意k≥3,f(x)都有k倍不动点,求实数a的取值范围;
(3)设m,n(m<n)为f(x)的2倍不动点,且函数f(x)在x∈[m,n]时值域为[2m,2n],求a的取值范围;
(4)函数f(x)在x∈[m,n](m<n)时单调,且值域恰为[2m,2n],求a的取值范围.
考点:函数与方程的综合运用
专题:计算题,函数的性质及应用
分析:(1)令f(x)=x,解出方程的两根,令两根大于等于0,小于等于2,解得即可;
(2)令f(x)=kx,判别式△≥0恒成立,讨论对称轴与3的关系,解不等式,即可得到a的范围;
(3)令f(x)=2x,判别式大于0,区间为[m,n]为增区间,考虑对称轴与区间的关系,解得即可;
(4)若为增,考虑对称轴与区间的关系和判别式大于0,即有-a-
≤-
;考虑为减,则f(m)=2n,f(n)=2m,作差可得,m+n=-3-2a,代入f(m)=2n,再由判别式大于等于0,及区间在对称轴的左边,解不等式即可得到.
(2)令f(x)=kx,判别式△≥0恒成立,讨论对称轴与3的关系,解不等式,即可得到a的范围;
(3)令f(x)=2x,判别式大于0,区间为[m,n]为增区间,考虑对称轴与区间的关系,解得即可;
(4)若为增,考虑对称轴与区间的关系和判别式大于0,即有-a-
| 1 |
| 2 |
| 1 |
| 8 |
解答:
解:(1)f(x)=x2+(2a+1)x+a2+a区间[0,2]有两个相异的1倍不动点,
则x2+2ax+a2+a=0区间[0,2]有两个相异的实根,
即有x=-a±
∈[0,2],
由0≤-a+
≤2,解得,-1≤a<0;
由0≤-a-
≤2,解得,-4≤a≤-1.
则a=-1,此时两个不动点为0,2;
(2)对任意k≥3,f(x)都有k倍不动点,即有
f(x)=x2+(2a+1)x+a2+a=kx恒有解,
即方程x2+(2a+1-k)x+a2+a=0恒有解.
则判别式△≥0恒成立,即(2a+1-k)2-4(a2+a)≥0,
若2a+1≥3即a≥1,且4(a2+a)≤0,则a无解,不成立;
若2a+1<3,即a<1,且4(a2+a)≤(2a+1-3)2,即有a≤
,
则有a≤
.
综上可得,a的取值范围为(-∞,
];
(3)由于m,n(m<n)为f(x)的2倍不动点,
则f(x)=2x有两个不相等的实根,即x2+(2a+1)x+a2+a=2x,
即有x2+(2a-1)x+a2+a=0,则由(2a-1)2-4(a2+a)>0,
解得,a<
;
函数f(x)在x∈[m,n]时值域为[2m,2n],
由于y=2x为增函数,则f(x)在[m,n]为单调增区间,即有f(m)=2m,f(n)=2n,
且-a-
≤m,f(x)的最小值为
=-
,
即有-
=-2a-1,解得,a=-
.
则a的取值范围为[-
,
);
(4)函数f(x)在x∈[m,n](m<n)时单调,且值域恰为[2m,2n],
若为增函数,则有f(m)=2m,f(n)=2n,
且-a-
≤m,f(x)的最小值为
=-
,
即有2m≥-
,即m≥-
,则-a-
≤-
,解得,a≥-
;
若为减函数,则有f(m)=2n,f(n)=2m,
即为m2+(2a+1)m+a2+a=2n,n2+(2a+1)n+a2+a=2m,
由于m<n,相减得,m+n=-3-2a,
即有m2+(2a+3)m+a2+5a+6=0有解,则判别式(2a+3)2-4(a2+5a+6)≥0,
解得,a≤-
,
又2m≤-
,即m≤-
,且-a-
≥n>m,即有-a-
≥-
,解得,a≤-
.
则有a≤-
成立.
综上可得,a≥-
或a≤-
.
则x2+2ax+a2+a=0区间[0,2]有两个相异的实根,
即有x=-a±
| -a |
由0≤-a+
| -a |
由0≤-a-
| -a |
则a=-1,此时两个不动点为0,2;
(2)对任意k≥3,f(x)都有k倍不动点,即有
f(x)=x2+(2a+1)x+a2+a=kx恒有解,
即方程x2+(2a+1-k)x+a2+a=0恒有解.
则判别式△≥0恒成立,即(2a+1-k)2-4(a2+a)≥0,
若2a+1≥3即a≥1,且4(a2+a)≤0,则a无解,不成立;
若2a+1<3,即a<1,且4(a2+a)≤(2a+1-3)2,即有a≤
| 1 |
| 3 |
则有a≤
| 1 |
| 3 |
综上可得,a的取值范围为(-∞,
| 1 |
| 3 |
(3)由于m,n(m<n)为f(x)的2倍不动点,
则f(x)=2x有两个不相等的实根,即x2+(2a+1)x+a2+a=2x,
即有x2+(2a-1)x+a2+a=0,则由(2a-1)2-4(a2+a)>0,
解得,a<
| 1 |
| 8 |
函数f(x)在x∈[m,n]时值域为[2m,2n],
由于y=2x为增函数,则f(x)在[m,n]为单调增区间,即有f(m)=2m,f(n)=2n,
且-a-
| 1 |
| 2 |
| 4(a2+a)-(2a+1)2 |
| 4 |
| 1 |
| 4 |
即有-
| 1 |
| 4 |
| 3 |
| 8 |
则a的取值范围为[-
| 3 |
| 8 |
| 1 |
| 8 |
(4)函数f(x)在x∈[m,n](m<n)时单调,且值域恰为[2m,2n],
若为增函数,则有f(m)=2m,f(n)=2n,
且-a-
| 1 |
| 2 |
| 4(a2+a)-(2a+1)2 |
| 4 |
| 1 |
| 4 |
即有2m≥-
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
若为减函数,则有f(m)=2n,f(n)=2m,
即为m2+(2a+1)m+a2+a=2n,n2+(2a+1)n+a2+a=2m,
由于m<n,相减得,m+n=-3-2a,
即有m2+(2a+3)m+a2+5a+6=0有解,则判别式(2a+3)2-4(a2+5a+6)≥0,
解得,a≤-
| 15 |
| 8 |
又2m≤-
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
| 3 |
| 8 |
则有a≤-
| 15 |
| 8 |
综上可得,a≥-
| 3 |
| 8 |
| 15 |
| 8 |
点评:本题考查新定义的理解和运用,考查二次方程和二次函数的关系,考查函数的定义域和值域的关系,及函数的单调性的运用,考查运算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列函数为奇函数的是( )
| A、x2+2x | ||
| B、2cosx+1 | ||
| C、x3sinx | ||
D、2x-
|
若两个二面角的面分别垂直且它们的棱互相平行,则它们的角度之间的关系为( )
| A、相等 | B、互补 |
| C、相等或互补 | D、无法确定 |
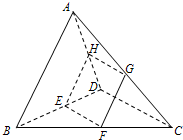 三棱锥A-BCD中,面ACD与面BCD均为正三角形,点E,F,G,H分别为BD,BC,AC,AD中点
三棱锥A-BCD中,面ACD与面BCD均为正三角形,点E,F,G,H分别为BD,BC,AC,AD中点