题目内容
有324，243，270三个数，则它们的最大公约数是 ．
考点：用辗转相除计算最大公约数
专题：计算题,算法和程序框图
分析：两次应用辗转相除法：先求出324与243的最大公约数是81，再求出81与270的最大公约数27即可．
解答：
解：用辗转相除法先求324与243的最大公约数．
∵324=243×1+81，243=81×3+0，
∴324与243的最大公约数是81；
再求81与270的最大公约数
∵270=81×3+27，81=27×3+0，
∴81与270的最大公约数是27，
故324，243，270三个数的最大公约数是27．
故答案为：27．
∵324=243×1+81，243=81×3+0，
∴324与243的最大公约数是81；
再求81与270的最大公约数
∵270=81×3+27，81=27×3+0，
∴81与270的最大公约数是27，
故324，243，270三个数的最大公约数是27．
故答案为：27．
点评：本题考查辗转相除法，这是案例中的一种题目，这种题目解题时需要有耐心，认真计算，不要在数字运算上出错，属于基础题．
练习册系列答案
相关题目
如图，AB是⊙O的一条直径，过A作⊙O的切线，在切线上取一点C，使AC=AB，连接OC，与⊙O交于点D，BD的延长线与AC交于点E，求证：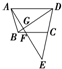
如图，梯形ABCD中，E是DC延长线上一点，AE分别交BD于G，交BC于F．则下列结论：