题目内容
若不等式4x2+9y2≥2kxy对一切正数x，y恒成立，则整数k的最大值为 ．
考点：函数恒成立问题
专题：函数的性质及应用
分析：将不等式进行转化为基本不等式形式，然后利用基本不等式的解法即可得到结论．
解答：
解：不等式4x2+9y2≥2kxy对一切正数x，y恒成立，
则等价为
=
+
≥2k恒成立，
∵
+
≥2
=2×6=12当且仅当
=
，
即2x=3y时取等号，
∴要使
=
+
≥2k恒成立，
则2k≤12，
∵k是整数，
∴整数k的最大值为3，
故答案为：3．
则等价为
| 4x2+9y2 |
| xy |
| 4x |
| y |
| 9y |
| x |
∵
| 4x |
| y |
| 9y |
| x |
|
| 4x |
| y |
| 9y |
| x |
即2x=3y时取等号，
∴要使
| 4x2+9y2 |
| xy |
| 4x |
| y |
| 9y |
| x |
则2k≤12，
∵k是整数，
∴整数k的最大值为3，
故答案为：3．
点评：本题注意考查不等式恒成立，利用基本不等式的解法是解决本题的关键．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
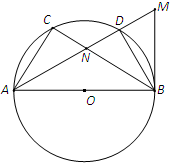如图，AB是⊙O的一条直径，C，D是⊙O上不同于A，B的两点，过B作⊙O的切线与AD的延长线相交于点M，AD与BC相交于N点，BN=BM．
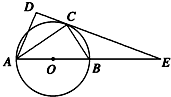如图，在△ABC和△ACD中，∠ACB=∠ADC=90°，∠BAC=∠CAD，⊙O是以AB为直径的圆，DC的延长线与AB的延长线交于点E．若EB=6，EC=6