题目内容
如图，AB是⊙O的一条直径，过A作⊙O的切线，在切线上取一点C，使AC=AB，连接OC，与⊙O交于点D，BD的延长线与AC交于点E，求证：（Ⅰ）∠CDE=∠DAE；
（Ⅱ）AE=CD．
考点：与圆有关的比例线段,弦切角
专题：直线与圆
分析：（Ⅰ）由已知条件，利用弦切角定理能证明∠CDE=∠DAE．
（Ⅱ）由已知条件，推导出△CDE∽△CAD，进而得到△ADE∽△BAE，由此能够证明AE=CD．
（Ⅱ）由已知条件，推导出△CDE∽△CAD，进而得到△ADE∽△BAE，由此能够证明AE=CD．
解答：
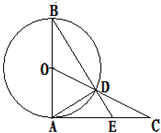证明：（Ⅰ）如图，∵∠CDE=∠ODB=∠OBD，
AC与⊙O切于点A，AD是弦，
∴∠DAE=∠OBD
∴∠CDE=∠DAE． …（5分）
（Ⅱ）∵∠CDE=∠CAD，∠C=∠C，
∴△CDE∽△CAD
∴
=
，∴CD=AC•
…①
而△ADE∽△BAE，∴
=
…②
由①②得CD=AC•
又∵AC=AB，∴AE=CD． …（10分）
证明：（Ⅰ）如图，∵∠CDE=∠ODB=∠OBD，AC与⊙O切于点A，AD是弦，
∴∠DAE=∠OBD
∴∠CDE=∠DAE． …（5分）
（Ⅱ）∵∠CDE=∠CAD，∠C=∠C，
∴△CDE∽△CAD
∴
| CD |
| AC |
| DE |
| AD |
| DE |
| AD |
而△ADE∽△BAE，∴
| DE |
| AD |
| AE |
| AB |
由①②得CD=AC•
| AE |
| AB |
又∵AC=AB，∴AE=CD． …（10分）
点评：本题考查角的相等、线段长相等的证明，是中档题，解题时要注意弦切角定理、相似三角形等知识点的合理运用．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
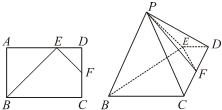如图，在矩形ABCD中，点E为边AD上的点，点F为边CD的中点，AB=AE=
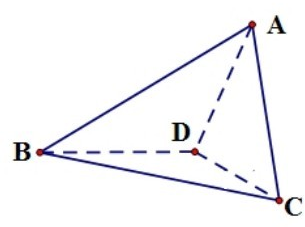已知四面体ABCD，∠ADB=∠CDB=120°，且平面ABD⊥平面BCD．
如图，在四棱锥P-ABCD中，底面ABCD是边长为1的菱形，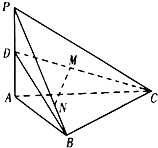
如图，在四面体P-ABC中，PA⊥平面ABC，AB⊥BC，PA=2，AC=2
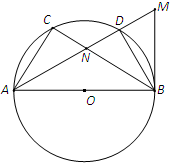如图，AB是⊙O的一条直径，C，D是⊙O上不同于A，B的两点，过B作⊙O的切线与AD的延长线相交于点M，AD与BC相交于N点，BN=BM．