题目内容
在△ABC中,∠ABC=
,AB=
,BC=3,则sin∠BAC= .
| π |
| 4 |
| 2 |
考点:正弦定理
专题:三角函数的求值
分析:利用余弦定理列出关系式,将各自的值代入求出b的值,再利用正弦定理即可求出sin∠BAC的值.
解答:
解:∵在△ABC中,∠ABC=
,AB=c=
,BC=a=3,
∴由余弦定理得:b2=a2+c2-2accos∠ABC=9+2-6=5,即b=
,
则由正弦定理
=
得:sin∠BAC=
=
.
故答案为:
| π |
| 4 |
| 2 |
∴由余弦定理得:b2=a2+c2-2accos∠ABC=9+2-6=5,即b=
| 5 |
则由正弦定理
| a |
| sin∠BAC |
| b |
| sin∠ABC |
3×
| ||||
|
3
| ||
| 10 |
故答案为:
3
| ||
| 10 |
点评:此题考查了正弦、余弦定理,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
把6个人平均分成两组,再从各组中分别选出正组长1名和副组长1名,则不同的选法种数是( )
| A、720 | B、360 |
| C、120 | D、60 |
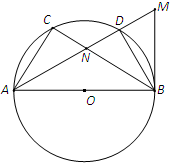 如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.
如图,AB是⊙O的一条直径,C,D是⊙O上不同于A,B的两点,过B作⊙O的切线与AD的延长线相交于点M,AD与BC相交于N点,BN=BM.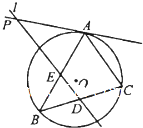 如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为
如图,△ABC内接于⊙O,过BC中点D作平行于AC的直线l,l交AB于E,交⊙O在A点处的切线于点P,若PE=6,ED=3,则AE的长为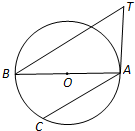
 如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=
如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若CD=