题目内容
已知a,b为两条互不垂直的异面直线,a?α,b?β,下列四个结论中,不可能成立的是( )
| A、b∥α | B、b⊥α |
| C、β∥α | D、β⊥α |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:由已知得在B中:b⊥α,a?α,从而b⊥a,与a,b为两条互不垂直的异面直线矛盾,故B不可能成立.
解答:
解:由a,b为两条互不垂直的异面直线,a?α,b?β,知:
在A中:b∥α,a?α,a与b异面但不垂直,这种情况存在,故A正确;
在B中:b⊥α,a?α,从而b⊥a,与a,b为两条互不垂直的异面直线矛盾,故B错误;
在C中,β∥α,a?α,b?β,a,b为两条互不垂直的异面直线,这种情况存在,故C正确;
在D中:β⊥α,a?α,b?β,a,b为两条互不垂直的异面直线,这种情况存在,故D正确.
故选:B.
在A中:b∥α,a?α,a与b异面但不垂直,这种情况存在,故A正确;
在B中:b⊥α,a?α,从而b⊥a,与a,b为两条互不垂直的异面直线矛盾,故B错误;
在C中,β∥α,a?α,b?β,a,b为两条互不垂直的异面直线,这种情况存在,故C正确;
在D中:β⊥α,a?α,b?β,a,b为两条互不垂直的异面直线,这种情况存在,故D正确.
故选:B.
点评:本题考查命题真假的判断,是中档题,解题时要注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
在(1+x)6(1+y)4的展开式中,xy2项的系数为( )
| A、45 | B、36 | C、60 | D、120 |
在数列{an}中,已知an=
(c∈R),则对于任意正整数n有( )
| n+c |
| n+1 |
| A、an<an+1 |
| B、an与an+1的大小关系和c有关 |
| C、an>an+1 |
| D、an与an+1的大小关系和n有关 |
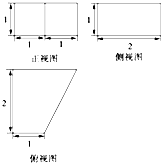
 图①是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成图②所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是
图①是边长为30cm的正方形纸板,裁掉阴影部分后将其折叠成图②所示的长方体盒子,已知该长方体的宽是高的2倍,则它的体积是