题目内容

已知向量
a
，
b
满足|
a
|=1，|
b
|=
2

（Ⅰ）若
a
•
b
=
2
2
，求
a
与
b
的夹角
（Ⅱ）若
a
与
b
的夹角为135°，求|
a
+
b
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：（I）由|
a
|=1，|
b
|=
2
，
a
•
b
=
2
2
，利用向量夹角公式即可得出．
（II）利用数量积运算性质可得|
a
+
b
|=
a
2+
b
2+2
a
•
b
，即可得出．
解答： 解：（I）∵|
a
|=1，|
b
|=
2
，
a
•
b
=
2
2
，
∴cos＜
a
，
b
＞=
a
•
b
|
a
||
b
|
=
2
2
1×
2
=
1
2
，
∴＜
a
，
b
＞=60°．
（II）|
a
+
b
|=
a
2+
b
2+2
a
•
b
=
1+(
2
)2+2×1×
2
×cos135°
=1..
点评：本题考查了向量夹角公式与数量积运算性质，考查了计算能力，属于基础题．
练习册系列答案
相关题目
已知：sinαcosβ+cosαsinβ=sin2α+sin2β，求证：α+β=
π
2
．
已知a，b为两条互不垂直的异面直线，a?α，b?β，下列四个结论中，不可能成立的是（　　）
A、b∥αB、b⊥α
C、β∥αD、β⊥α
若点（2a，a-1）在圆x2+（y-1）2=5的内部，则a的取值范围是
 
．
已知tanα=3，求下列各式的值：
（1）
3
cosα-sinα
3
cosα+sinα
；
（2）2sin2α-3sinαcosα；
（3）
5sin3α+cosα
2cos3α+sin2αcosα
．
数列{an}的通项公式为an=logn+1（n+2），则它前14项的积为 4．
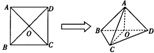已知正方形ABCD的边长为1，AC∩BD=O，将正方形ABCD沿对角线折起，使AC=1，得到三棱锥A-BCD，如图所示．
（1）求证：AO⊥平面BCD；
（2）求平面ABC与平面BCD夹角的余弦值．
某中学在高二年级开设大学先修课程《线性代数》，共有50名同学选修，其中男同学30名，女同学20名．为了对这门课程的教学效果进行评估，学校按性别采用分层抽样的方法抽取5人进行考核．
（I）求抽取的5人中男、女同学的人数；
（II）考核前，评估小组打算从抽取的5人中随机选出2名同学进行访谈，求选出的两名同学中恰有一名女同学的概率．
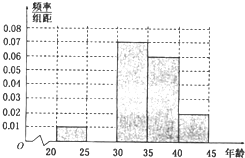在某市“创建文明城市”活动中，对800名志愿者的年龄抽样调查统计后得到频率分布直方图（如图），但是年龄组为[25，30）的数据不慎丢失，据此估计这800名志愿者年龄在[25，30）的人数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网