题目内容

8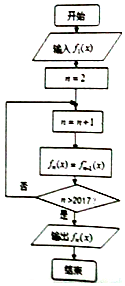．执行如图的程序框图，当n≥2，n∈Z时，fn（x）表示fn-1（x）的导函数，若输入函数f1（x）=sinx-cosx，则输出的函数fn（x）可化为（　　）
A．$\sqrt{2}$sin（x+$\frac{π}{4}$）B．$\sqrt{2}$sin（x-$\frac{π}{4}$）C．-$\sqrt{2}$sin（x+$\frac{π}{4}$）D．-$\sqrt{2}$sin（x-$\frac{π}{4}$）

分析 先根据流程图弄清概括程序的功能，然后计算分别f1（x），f2（x）、f3（x）、f4（x）、f5（x），得到周期，从而求出f2017（x）的解析式．

解答 解：由框图可知n=2018时输出结果f2017（x），
由于f1（x）=sinx-cosx，
f2（x）=sinx+cosx，
f3（x）=-sinx+cosx，
f4（x）=-sinx-cosx，
f5（x）=sinx-cosx，
…
所以f2017（x）=f4×504+1（x）=f1（x）=sinx-cosx=$\sqrt{2}$sin（x-$\frac{π}{4}$）．
故选：B．

点评 本题主要考查循环结构的程序框图的应用，解题的关键是识图，特别是循环结构的使用、同时考查周期性及三角变换，属于基础题．

练习册系列答案
相关题目
18．设椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1，（0＜b＜2）的右焦点为F，右顶点为A，已知$\frac{|FA|}{|OF|}$+$\frac{|FA|}{|OA|}$=3e，其中O为原点，e为椭圆的离心率．
（Ⅰ）求椭圆的方程；
（Ⅱ）设过点A的直线l与椭圆交于点B（B不在x轴上），若点H（0，$\frac{4}{3}$），以BH为直径的圆过F点，求直线l的斜率．
19．已知点F为椭圆$E：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左焦点，且两焦点与短轴的一个顶点构成一个等边三角形，直线$\frac{x}{4}+\frac{y}{2}=1$与椭圆E有且仅有一个交点M．
（Ⅰ）求椭圆E的方程；
（Ⅱ）设直线$\frac{x}{4}+\frac{y}{2}=1$与y轴交于P，过点P的直线与椭圆E交于两不同点A，B，若λ|PM|2=|PA|•|PB|，求实数λ的取值范围．
16．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的焦点为F1，F2，若椭圆上存在满足$\overrightarrow{P{F_1}}•\overrightarrow{P{F_2}}=\frac{1}{2}{b^2}$的点P，则椭圆的离心率的范围是$[\frac{{\sqrt{3}}}{3}，1）$．
3．已知函数f（x）=|x-a|．
（Ⅰ）若a=1，解不等式：f（x）≥4-|x-3|；
（Ⅱ）若f（x）≤1的解集为[0，2]，$\frac{1}{m}+\frac{1}{2n}=a$（m＞0，n＞0），求mn的最小值．
13．已知f（x）=$\sqrt{3}$sinx•cosx+cos2x，锐角△ABC的三个角A，B，C所对的边分别为a，b，c．
（Ⅰ）求函数f（x）的最小正周期和单调递增区间；
（Ⅱ）若f（C）=1，求m=$\frac{{a}^{2}+{b}^{2}+{c}^{2}}{ab}$的取值范围．
20．一个几何体的三视图如图所示，则它的体积为（　　）
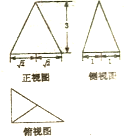
A．$2\sqrt{2}$B．$2\sqrt{3}$C．$6\sqrt{2}$D．$6\sqrt{3}$
17．将参加数学竞赛决赛的500名同学编号为：001，002，…，500，采用系统抽样的方法抽取一个容量为50的样本，且随机抽的号码为003，这500名学生分别在三个考点考试，从001到200在第一考点，从201到355在第二考点，从356到500在第三考点，则第二考点被抽中的人数为（　　）
A．14B．15C．16D．17
18．已知定义域为{x|x≠0}的偶函数f（x），其导函数为f′（x），对任意正实数x满足xf′（x）＞-2f（x），若g（x）=x2f（x），则不等式g（x）＜g（1）的解集是（　　）
A．（-∞，1）B．（-∞，0）∪（0，1）C．（-1，1）D．（-1，0）∪（0，1）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网