题目内容
18.设椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(0<b<2)的右焦点为F,右顶点为A,已知$\frac{|FA|}{|OF|}$+$\frac{|FA|}{|OA|}$=3e,其中O为原点,e为椭圆的离心率.(Ⅰ)求椭圆的方程;
(Ⅱ)设过点A的直线l与椭圆交于点B(B不在x轴上),若点H(0,$\frac{4}{3}$),以BH为直径的圆过F点,求直线l的斜率.
分析 (1)根据题意,可得$\frac{a-c}{c}$+$\frac{a-c}{a}$=3×$\frac{c}{a}$,变形可得a2=4c2,结合椭圆的标准方程可得a2=4以及c2=1,进而计算可得b2的值,将其代入椭圆的标准方程,计算可得答案;
(2)根据题意,设出直线l的斜率以及方程,联立直线与椭圆的方程,解可得B的坐标,结合F、H的坐标可得向量$\overrightarrow{HF}$与$\overrightarrow{BF}$的坐标,分析可得BH为直径的圆过点F,得$\overrightarrow{BF}$•$\overrightarrow{HF}$=0,进而有1×$\frac{9-4{k}^{2}}{4{k}^{2}+3}$-($\frac{4}{3}$)×$\frac{12k}{4{k}^{2}+3}$)=0,解可得k的值,即得答案.
解答 解:(1)根据题意,$\frac{|FA|}{|OF|}$+$\frac{|FA|}{|OA|}$=3e,有$\frac{a-c}{c}$+$\frac{a-c}{a}$=3×$\frac{c}{a}$,变形可得a2-c2=3c2,即a2=4c2,
又由a2=4,则c2=1,
b2=a2-c2=3,
故椭圆的方程为:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)设直线l的斜率为k,(k≠0),则直线l的方程为y=k(x-2);
设B(xB,yB),
联立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-2)}\end{array}\right.$,消去y整理可得(4k2+3)x2-16k2x+16k2-12=0,
解可得x=2或x=$\frac{8{k}^{2}-6}{4{k}^{2}+3}$,
由题意可得xB=$\frac{8{k}^{2}-6}{4{k}^{2}+3}$,yB=$\frac{-12k}{4{k}^{2}+3}$,
由(1)可得:F(1,0),又由H(0,$\frac{4}{3}$),
则有$\overrightarrow{HF}$=(1,-$\frac{4}{3}$),$\overrightarrow{BF}$=($\frac{9-4{k}^{2}}{4{k}^{2}+3}$,$\frac{12k}{4{k}^{2}+3}$),
以BH为直径的圆过点F,得$\overrightarrow{BF}$•$\overrightarrow{HF}$=0,
即1×$\frac{9-4{k}^{2}}{4{k}^{2}+3}$-($\frac{4}{3}$)×$\frac{12k}{4{k}^{2}+3}$)=0,
解可得k=-$\frac{9}{2}$或k=$\frac{1}{2}$.
点评 本题考查椭圆与直线的位置关系,涉及椭圆的简单几何性质以及标准方程的应用,关键是依据题意,求出椭圆的方程.

| A. | 若m∥α,α∩β=n,则 m∥n | B. | 若m∥α,m⊥n,则n⊥α | ||
| C. | 若m⊥α,n⊥α,则m∥n | D. | 若m?α,n?β,α⊥β,则m⊥n |
| A. | 事件A的概率P(A)必有0<P(A)<1 | |
| B. | 事件A的概率P(A)=0.999,则事件A是必然事件 | |
| C. | 用某种药物对患有胃溃疡的500名病人治疗,结果有380人有明显的疗效,现有胃溃疡的病人服用此药,则估计其有明显的疗效的可能性为76% | |
| D. | 某奖券中奖率为50%,则某人购买此券10张,一定有5张中奖 |
| A. | $\frac{1}{9}$ | B. | $\frac{5}{36}$ | C. | $\frac{3}{18}$ | D. | $\frac{1}{72}$ |
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
| A. | 1 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 4 |
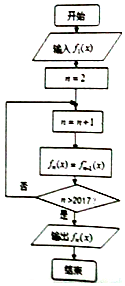 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.