题目内容
19.已知点F为椭圆$E:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点,且两焦点与短轴的一个顶点构成一个等边三角形,直线$\frac{x}{4}+\frac{y}{2}=1$与椭圆E有且仅有一个交点M.(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线$\frac{x}{4}+\frac{y}{2}=1$与y轴交于P,过点P的直线与椭圆E交于两不同点A,B,若λ|PM|2=|PA|•|PB|,求实数λ的取值范围.
分析 (Ⅰ)由题意可得a,b与c的关系,化椭圆方程为$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,联立直线方程与椭圆方程,由判别式为0求得c,则椭圆方程可求;
(Ⅱ)由(Ⅰ)求得M坐标,得到|PM|2,当直线l与x轴垂直时,直接由λ|PM|2=|PA|•|PB|求得λ值;当直线l与x轴不垂直时,设直线l的方程为y=kx+2,联立直线方程与椭圆方程,利用判别式大于0求得k的取值范围,再由根与系数的关系,结合λ|PM|2=|PA|•|PB|,把λ用含有k的表达式表示,则实数λ的取值范围可求.
解答 解:(Ⅰ)由题意,得$a=2c,b=\sqrt{3}c$,则椭圆E为:$\frac{x^2}{{4{c^2}}}+\frac{y^2}{{3{c^2}}}=1$,
联立$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}={c^2}\\ \frac{x}{4}+\frac{y}{2}=1\end{array}\right.$,得x2-2x+4-3c2=0,
∵直线$\frac{x}{4}+\frac{y}{2}=1$与椭圆E有且仅有一个交点M,
∴△=4-4(4-3c2)=0,得c2=1,
∴椭圆E的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$;
(Ⅱ)由(Ⅰ)得$M({1,\frac{3}{2}})$,
∵直线$\frac{x}{4}+\frac{y}{2}=1$与y轴交于P(0,2),∴${|{PM}|^2}=\frac{5}{4}$,
当直线l与x轴垂直时,$|{PA}|•|{PB}|=({2+\sqrt{3}})({2-\sqrt{3}})=1$,
由λ|PM|2=|PA|•|PB|,得$λ=\frac{4}{5}$,
当直线l与x轴不垂直时,设直线l的方程为y=kx+2,A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+2}\\{3{x}^{2}+4{y}^{2}-12=0}\end{array}\right.$,得(3+4k2)x2+16kx+4=0,
依题意得,${x_1}{x_2}=\frac{4}{{3+4{k^2}}}$,且△=48(4k2-1)>0,
∴$|{PA}||{PB}|=({1+{k^2}}){x_1}{x_2}=({1+{k^2}})•\frac{4}{{3+4{k^2}}}=1+\frac{1}{{3+4{k^2}}}=\frac{5}{4}λ$,
∴$λ=\frac{4}{5}({1+\frac{1}{{3+4{k^2}}}})$,
∵${k^2}>\frac{1}{4}$,∴$\frac{4}{5}<λ<1$,
综上所述,λ的取值范围是$[{\frac{4}{5},1})$.
点评 本题考查椭圆的简单性质,考查了直线与椭圆位置关系的应用,体现了“分类讨论”的数学思想方法,属中档题.

| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
| A. | 1 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 4 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | (1,+∞) | B. | (-∞,1) | C. | (e,+∞) | D. | (-∞,e) |
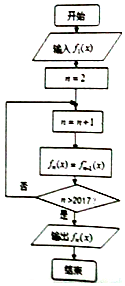 执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )
执行如图的程序框图,当n≥2,n∈Z时,fn(x)表示fn-1(x)的导函数,若输入函数f1(x)=sinx-cosx,则输出的函数fn(x)可化为( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
 随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,每售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如右图所示.已知电商为下一个销售季度筹备了130吨该商品.现以x(单位:吨,100≤x≤150)表示下一个销售季度的市场需求量,T(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.