题目内容
20．一个几何体的三视图如图所示，则它的体积为（ ）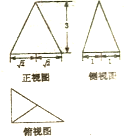
| A． | $2\sqrt{2}$ | B． | $2\sqrt{3}$ | C． | $6\sqrt{2}$ | D． | $6\sqrt{3}$ |
分析 由已知中的三视图，可得该几何体是一个以俯视图为底面的三棱锥，代入棱锥体积公式，可得答案．
解答 解：由已知中的三视图，可得该几何体是一个以俯视图为底面的三棱锥，
底面面积S=$\frac{1}{2}$×$（\sqrt{2}+\sqrt{2}）$×（1+1）=2$\sqrt{2}$，
棱锥的高h=3，
故体积V=$\frac{1}{3}Sh$=2$\sqrt{2}$，
故选：A
点评 本题考查的知识点是棱锥的体积和表面积，简单几何体的三视图，难度中档．
练习册系列答案
相关题目
10．若函数$f（x）={x^2}+ax+\frac{1}{x}$在$（{\frac{1}{2}\;\;，\;\;1}）$内任取两个实数p，q，且p≠q，不等式$\frac{f（p）-f（q）}{p-q}＞0$恒成立，则a的取值范围是（ ）
| A． | [-1，0] | B． | [-1，+∞） | C． | [0，3] | D． | [3，+∞） |
11．已知函数f（x）=x-alnx，当x＞1时，f（x）＞0恒成立，则实数a的取值范围是（ ）
| A． | （1，+∞） | B． | （-∞，1） | C． | （e，+∞） | D． | （-∞，e） |
8．
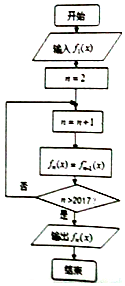执行如图的程序框图，当n≥2，n∈Z时，fn（x）表示fn-1（x）的导函数，若输入函数f1（x）=sinx-cosx，则输出的函数fn（x）可化为（ ）
执行如图的程序框图，当n≥2，n∈Z时，fn（x）表示fn-1（x）的导函数，若输入函数f1（x）=sinx-cosx，则输出的函数fn（x）可化为（ ）| A． | $\sqrt{2}$sin（x+$\frac{π}{4}$） | B． | $\sqrt{2}$sin（x-$\frac{π}{4}$） | C． | -$\sqrt{2}$sin（x+$\frac{π}{4}$） | D． | -$\sqrt{2}$sin（x-$\frac{π}{4}$） |
15．已知集合P={x|-1≤x≤1}，M={a}，若P∩M=∅，则a取值范围是（ ）
| A． | （-∞，-1] | B． | [1，+∞） | C． | [-1，1] | D． | （-∞，-1）∪（1，+∞） |
10．已知数列{an}为等比数列，Sn为其前n项和，且${S_n}=2017×{2016^n}-2018t$，则t=（ ）
| A． | $\frac{2015}{2016}$ | B． | $\frac{2016}{2017}$ | C． | $\frac{2017}{2018}$ | D． | $\frac{2018}{2019}$ |