Question

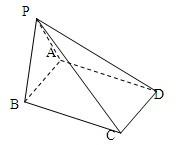如图，四棱锥P-ABCD的底面是AB=2，BC=

2

的矩形，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD，求PC与面PAD所成角的大小．

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：取AB中点O，以OB为x轴，OP为z轴，建立空间直角坐标系，利用向量法能求出PC与面PAD所成角为45°．

解答： 解：取AB中点O，
以OB为x轴，OP为z轴，建立空间直角坐标系，
P（0，0，

3

），C（1，

2

，0），
A（-1，0，0），D（-1，

2

，0），

PC

=（1，

2

，-

3

），

PA

=（-1，0，-

3

），

PD

=（-1，

2

，-

3

），
设平面PAD的法向量

n

=（x，y，z），
则

n • PA =-x- 3 z=0 n • PD =-x+ 2 y- 3 z=0

，
取x=

3

，得

n

=（

3

，0，-1），
设PC与面PAD所成角为θ，
sinθ=|cos＜

PC

，

n

＞|=|

3 + 3

6 •2

|=

2

2

，
∴θ=45°，
∴PC与面PAD所成角为45°．

点评：本题考查直线与平面所成角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．