题目内容
已知A(2,-3),B(-3,-2),直线l:ax+y-a-1=0与线段AB相交,则a的取值范围为 .
考点:恒过定点的直线
专题:直线与圆
分析:直线l:ax+y-a-1=0经过 C(1,1)点,斜率k=-a,kBC=-a=
=
,kAC=-a=
=-4,由此利用数形结合法能求出a的取值范围.
| 1+2 |
| 1+3 |
| 3 |
| 4 |
| 1+3 |
| 1-2 |
解答:
解:直线l:ax+y-a-1=0经过 C(1,1)点,斜率k=-a,
讨论临界点:
当直线l经过B点(-3,-2)时,
kBC=-a=
=
,
结合图形知-a∈(
,+∞)成立,∴a∈(-∞,-
);
当直线l经过A点(2,-3)时,
kAC=-a=
=-4,
结合图形知-a∈(-∞,-4),∴a∈(4,+∞).
综上a∈(-∞,-
)∪(4,+∞).
故答案为:(-∞,-
)∪(4,+∞).

讨论临界点:
当直线l经过B点(-3,-2)时,
kBC=-a=
| 1+2 |
| 1+3 |
| 3 |
| 4 |
结合图形知-a∈(
| 3 |
| 4 |
| 3 |
| 4 |
当直线l经过A点(2,-3)时,
kAC=-a=
| 1+3 |
| 1-2 |
结合图形知-a∈(-∞,-4),∴a∈(4,+∞).
综上a∈(-∞,-
| 3 |
| 4 |
故答案为:(-∞,-
| 3 |
| 4 |
点评:本题考查实数的取值范围的求法,是中档题,解题时要注意直线的斜率计算公式和数形结合思想的合理运用.

练习册系列答案
相关题目
等差数列{an}的前n项和为Sn,a2+a5+a7+a10的值是一个定值,则下列个数中也是定值的是( )
| A、S18 |
| B、S11 |
| C、S7 |
| D、S6 |
若θ∈(
,π),则
=( )
| π |
| 2 |
| 1-sin2θ |
| A、cosθ-sinθ |
| B、sinθ-cosθ |
| C、cosθ+sinθ |
| D、-cosθ-sinθ |
若命题“p∧q”为假,且“?q”为假,则( )
| A、“p∨q”为假 | B、p假 |
| C、p真 | D、不能判断q的真假 |
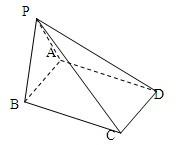 如图,四棱锥P-ABCD的底面是AB=2,BC=
如图,四棱锥P-ABCD的底面是AB=2,BC=