题目内容
函数y=-x2+x-1图象与x轴的交点个数是( )
| A、0 个 | B、1个 |
| C、2个 | D、无法确定 |
考点:二次函数的性质
专题:计算题,函数的性质及应用
分析:令y=-x2+x-1=0,可得x2-x+1=0,利用△=1-4<0,可得结论.
解答:
解:令y=-x2+x-1=0,可得x2-x+1=0,
∴△=1-4<0,
∴方程无解,
∴函数y=-x2+x-1图象与x轴的交点个数是0个.
故选:A.
∴△=1-4<0,
∴方程无解,
∴函数y=-x2+x-1图象与x轴的交点个数是0个.
故选:A.
点评:本题考查二次函数的性质,考查学生的计算能力,比较基础.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
若θ∈(
,π),则
=( )
| π |
| 2 |
| 1-sin2θ |
| A、cosθ-sinθ |
| B、sinθ-cosθ |
| C、cosθ+sinθ |
| D、-cosθ-sinθ |
若命题“p∧q”为假,且“?q”为假,则( )
| A、“p∨q”为假 | B、p假 |
| C、p真 | D、不能判断q的真假 |
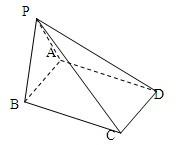 如图,四棱锥P-ABCD的底面是AB=2,BC=
如图,四棱锥P-ABCD的底面是AB=2,BC=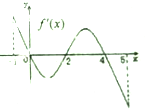 已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题:①函数f(x)在[0,2]是减函数;②如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;③函数y=f(x)-a有4个零点时1<a<2.其中真命题的个数是( )
已知函数f(x)的定义域为[-1,5],部分对应值如下表.f(x)的导函数y=f′(x)的图象如图所示.下列关于函数f(x)的命题:①函数f(x)在[0,2]是减函数;②如果当x∈[-1,t]时,f(x)的最大值是2,那么t的最大值为4;③函数y=f(x)-a有4个零点时1<a<2.其中真命题的个数是( )