题目内容
设集合A={(x,y)|a1x+b1x+c1=0},B={(x,y)|a2x+b2x+c2=0},则方程(a1x+b1x+c1)(a2x+b2x+c2)=0的解集为 .
考点:并集及其运算
专题:集合
分析:根据并集的定义判断即可得到结果.
解答:
解:∵集合A={(x,y)|a1x+b1x+c1=0},B={(x,y)|a2x+b2x+c2=0},
∴方程(a1x+b1x+c1)(a2x+b2x+c2)=0的解集为A∪B.
故答案为:A∪B
∴方程(a1x+b1x+c1)(a2x+b2x+c2)=0的解集为A∪B.
故答案为:A∪B
点评:此题考查了并集及其运算,熟练掌握并集的定义是解本题的关键.

练习册系列答案
相关题目
已知向量
,
满足|
|=1,|
|=4,且
•
≥2,则
与
的夹角的取值范围是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、[
| ||
B、(0,
| ||
C、[0,
| ||
D、[
|
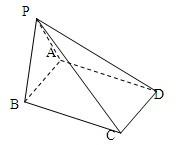 如图,四棱锥P-ABCD的底面是AB=2,BC=
如图,四棱锥P-ABCD的底面是AB=2,BC=