题目内容
计算下列各式的值：
（1）lg5lg20+（lg2）2；
（2）（log32+log92）•（log43+log83）+（
log33）2+ln
-lg1．
（1）lg5lg20+（lg2）2；
（2）（log32+log92）•（log43+log83）+（
| 1 |
| 2 |
| e |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的性质和运算法则求解．
解答：
解：（1）lg5lg20+（lg2）2
=lg 5lg（5×4）+（lg 2）2
=lg 5（lg 5+lg 4）+（lg 2）2
=（lg 5）2+lg 5lg 4+（lg 2）2
=（lg 5）2+2lg 5lg 2+（lg 2）2
=（lg 5+lg 2）2=1．
（2）（log32+log92）•（log43+log83）+（
log33）2+ln
-lg1
=log98•log64243+
+
-0
=
•
+
=
+
=2．
=lg 5lg（5×4）+（lg 2）2
=lg 5（lg 5+lg 4）+（lg 2）2
=（lg 5）2+lg 5lg 4+（lg 2）2
=（lg 5）2+2lg 5lg 2+（lg 2）2
=（lg 5+lg 2）2=1．
（2）（log32+log92）•（log43+log83）+（
| 1 |
| 2 |
| e |
=log98•log64243+
| 1 |
| 4 |
| 1 |
| 2 |
=
| 3lg2 |
| 2lg3 |
| 5lg3 |
| 6lg2 |
| 3 |
| 4 |
| 5 |
| 4 |
| 3 |
| 4 |
点评：本题考查对数值的求法，是基础题，解题时要注意对数的性质和运算法则的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
某几何体的三视图如图所示，则该几何体的体积为（ ）
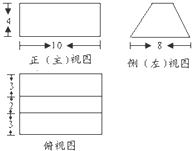
| A、240 | ||
| B、200 | ||
C、
| ||
D、
|
设函数y=f（x）的反函数是y=g（x），如果f（ab）=f（a）+f（b），则有（ ）
| A、g（ab）=g（a）•g（b） |
| B、g（a+b）=g（a）+g（b） |
| C、g（a+b）=g（a）•g（b） |
| D、g（ab）=g（a）+g（b） |
下列四组中的f（x），g（x），表示同一个函数的是（ ）
| A、f（x）=1，g（x）=x0 | ||
B、f（x）=x-1，g（x）=
| ||
C、f（x）=x，g（x）=（
| ||
D、f（x）=|1-2x|，g（x）=
|