题目内容
（Ⅰ）解不等式|2+x|+|2-x|≤4；
（Ⅱ）a，b∈R+，证明：a2+b2≥
（a+b）．
（Ⅱ）a，b∈R+，证明：a2+b2≥
| ab |
考点：不等式的证明,绝对值不等式的解法
专题：不等式的解法及应用,推理和证明
分析：（Ⅰ）通过对自变量x的取值范围的讨论，去掉绝对值符号，再解相应的不等式，最后取其并集即可；
（Ⅱ）利用作差法，作差后化积，分析判断证明即可．
（Ⅱ）利用作差法，作差后化积，分析判断证明即可．
解答：
解：（I）∵|2+x|+|2-x|=
…（2分），
∴由|2+x|+|2-x|≤4得：
或
或
，
解得x=-2或-2＜x≤2，
∴原不等式的解为：-2≤x≤2…（5分）
（II）证明：∵a2+b2-
(a+b)=a2-a
+b2-b
=a
(
-
)+b•
(
-
)
=（
-
）（a
-b
）
=（
-
）（
-
）（a+
+b）
=(
-
)2（a+
+b）≥0，
∴a2+b2≥
（a+b）…（10分）
|
∴由|2+x|+|2-x|≤4得：
|
|
|
解得x=-2或-2＜x≤2，
∴原不等式的解为：-2≤x≤2…（5分）
（II）证明：∵a2+b2-
| ab |
| ab |
| ab |
=a
| a |
| a |
| b |
| b |
| b |
| a |
=（
| a |
| b |
| a |
| b |
=（
| a |
| b |
| a |
| b |
| ab |
=(
| a |
| b |
| ab |
∴a2+b2≥
| ab |
点评：本题考查绝对值不等式的解法及不等式的证明，考查分类讨论思想与作差法证明不等式，属于中档题．
练习册系列答案
相关题目
设A={x|x2+x-6=0}，B={x|ax+1=0}，满足A?B，则a取值的集合是（ ）
A、{-
| ||||||
B、{-
| ||||||
C、{
| ||||||
D、{0，-
|
已知全集A={3，4，5}，B={1，3，6}，则A∩B=（ ）
| A、{3} |
| B、{4，5} |
| C、{1，6} |
| D、{2，4，5，7} |
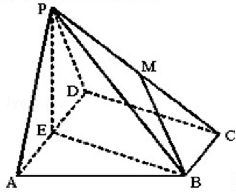如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，E为AD中点，M是棱PC的中点，PA=PD=2，BC=