题目内容
退休年龄延迟是平均预期寿命延长和人口老龄化背景下的一种趋势.某机构为了解某城市市民的年龄构成,从该城市市民中随机抽取年龄段在20~80岁(含20岁和80岁)之间的600人进行调查,并按年龄层次[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]绘制频率分布直方图,如图所示.若规定年龄分布在[20,40)岁的人为“青年人”,[40,60)为“中年人”,[60,80]为“老年人”.
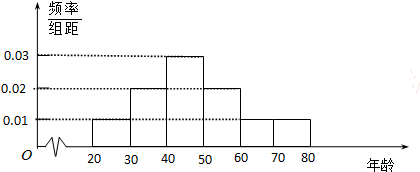
(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为X,求随机变量X的分布列和数学期望.

(Ⅰ)若每一组数据的平均值用该区间中点值来代替,试估算所调查的600人的平均年龄;
(Ⅱ)将上述人口分布的频率视为该城市在20-80年龄段的人口分布的概率.从该城市20-80年龄段市民中随机抽取3人,记抽到“老年人”的人数为X,求随机变量X的分布列和数学期望.
考点:离散型随机变量的期望与方差,频率分布直方图,离散型随机变量及其分布列
专题:概率与统计
分析:(Ⅰ)由频率分布直方图能估算所调查的600人的平均年龄.
(Ⅱ)由频率分布直方图知“老年人”所点频率为
,依题意,X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列和数学期望.
(Ⅱ)由频率分布直方图知“老年人”所点频率为
| 1 |
| 5 |
解答:
解:(Ⅰ)由频率分布直方图估算所调查的600人的平均年龄为:
25×0.1+35×0.2+45×0.3+55×0.2+65×0.1+75×0.1=48(岁).
(Ⅱ)由频率分布直方图知“老年人”所点频率为
,
∴从该城市20~80年龄段市民中随机抽取1人,抽到“老年人”的概率为
,
依题意,X的可能取值为0,1,2,3,
P(X=0)=
(
)3=
,
P(X=1)=
(
)(
)2=
,
P(X=2)=
(
)2(
)=
,
P(X=3)=
(
)3=
,
∴X的分布列为:
EX=0×
+1×
+2×
+3×
=
.
25×0.1+35×0.2+45×0.3+55×0.2+65×0.1+75×0.1=48(岁).
(Ⅱ)由频率分布直方图知“老年人”所点频率为
| 1 |
| 5 |
∴从该城市20~80年龄段市民中随机抽取1人,抽到“老年人”的概率为
| 1 |
| 5 |
依题意,X的可能取值为0,1,2,3,
P(X=0)=
| C | 0 3 |
| 4 |
| 5 |
| 64 |
| 125 |
P(X=1)=
| C | 1 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
P(X=2)=
| C | 2 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
P(X=3)=
| C | 3 3 |
| 1 |
| 5 |
| 1 |
| 125 |
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 3 |
| 5 |
点评:本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
下列函数中,既是偶函数,又在(0,+∞)上是单调减函数的是( )
A、y=x
| ||
| B、y=cosx | ||
| C、y=ln|x+1| | ||
| D、y=-2|x| |
设x,y满足约束条件
,则z=x+2y的最小值为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
若函数f(x)=cos2x+asinx在区间(
,
)是减函数,则a的取值范围是( )
| π |
| 6 |
| π |
| 2 |
| A、(2,4) |
| B、(-∞,2] |
| C、(-∞,4] |
| D、[4,+∞) |
已知点(x0,y0)不在曲线f(x,y)=0上,曲线f(x,y)+af(x0,y0)=0(a∈R,且a≠0)与曲线f(x,y)=0的交点有( )
| A、0个 | B、1个 | C、2个 | D、无数个 |