题目内容
下列函数中,既是偶函数,又在(0,+∞)上是单调减函数的是( )
A、y=x
| ||
| B、y=cosx | ||
| C、y=ln|x+1| | ||
| D、y=-2|x| |
考点:函数单调性的判断与证明,函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:运用常见函数的奇偶性和单调性以及定义,即可得到既是偶函数,又在(0,+∞)上是单调减函数的函数.
解答:
解:对于A,为幂函数,定义域为[0,+∞),不关于原点对称,则不具奇偶性,则A不满足;
对于B,为余弦函数,为偶函数,在(2kπ,2kπ+π)(k∈Z)上递减,则B不满足;
对于C,定义域为{x|x≠-1}不关于原点对称,则不具奇偶性,则C不满足;
对于D,定义域为R,f(-x)=-2|-x|=f(x),为偶函数,x>0时,y=-2x递减,则D满足.
故选D.
对于B,为余弦函数,为偶函数,在(2kπ,2kπ+π)(k∈Z)上递减,则B不满足;
对于C,定义域为{x|x≠-1}不关于原点对称,则不具奇偶性,则C不满足;
对于D,定义域为R,f(-x)=-2|-x|=f(x),为偶函数,x>0时,y=-2x递减,则D满足.
故选D.
点评:本题考查函数的奇偶性和单调性的判断,考查常见函数的奇偶性和单调性,考查运算和判断能力,属于基础题.

练习册系列答案
相关题目
设随机变量X等可能地取值1,2,3,…,10,则P(X<6)的值为( )
| A、0.3 | B、0.5 |
| C、0.6 | D、0.2 |
若曲线C1:x2+y2-4x=0与曲线C2:y(y-mx-x)=0有四个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
已知a,b为非零实数,且a<b,则下列命题成立的是( )
| A、a2<b2 | ||||
| B、a2b<a3 | ||||
C、
| ||||
D、
|
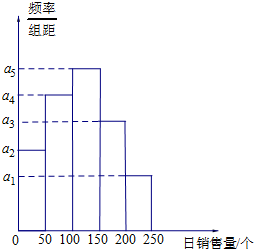 广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).
广州某商场根据以往某种商品的销售记录,绘制了日销售量的频率分布表(如表)和频率分布直方图(如图).