题目内容
已知点(x0,y0)不在曲线f(x,y)=0上,曲线f(x,y)+af(x0,y0)=0(a∈R,且a≠0)与曲线f(x,y)=0的交点有( )
| A、0个 | B、1个 | C、2个 | D、无数个 |
考点:曲线与方程
专题:计算题,直线与圆
分析:由已知f(x0,y0)≠0,设P(x1,y1)是f(x,y)=0上的点,则f(x1,y1)=0,判断P(x1,y1)不在曲线f(x,y)+af(x0,y0)=0上,即可得出结论.
解答:
解:由已知f(x0,y0)≠0,设P(x1,y1)是f(x,y)=0上的点,则f(x1,y1)=0,
但f(x1,y1)+af(x0,y0)≠0,即P(x1,y1)不在曲线f(x,y)+af(x0,y0)=0上.
故选A.
但f(x1,y1)+af(x0,y0)≠0,即P(x1,y1)不在曲线f(x,y)+af(x0,y0)=0上.
故选A.
点评:本题考查曲线与方程,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知x,y满足:x+y=
且x,y≠kπ+
(k∈Z),则(1+tanx)(1+tany)=( )
| π |
| 4 |
| π |
| 2 |
| A、-2 | B、2 | C、-1 | D、1 |
若曲线C1:x2+y2-4x=0与曲线C2:y(y-mx-x)=0有四个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
函数f(x)=1-2|x|的图象大致是( )
A、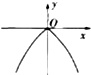 |
B、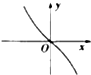 |
C、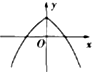 |
D、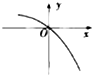 |
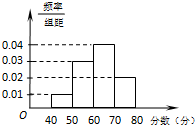 在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有
在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有