题目内容
设函数f(x)=ax2-x-2a,g(x)=ax+b,其中a,b∈Ra>0.已知f(1)+g(1)+3=0.
(1)求b的值;
(2)设集合A={y|y=f(x),x∈[-2,0]},B={y|y=g(x),x∈[-2,0]}且A∩B≠ϕ试求a的取值范围
(3)是否存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0?若存在,请求出a的值,若不存在,请说明理由.
(1)求b的值;
(2)设集合A={y|y=f(x),x∈[-2,0]},B={y|y=g(x),x∈[-2,0]}且A∩B≠ϕ试求a的取值范围
(3)是否存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0?若存在,请求出a的值,若不存在,请说明理由.
考点:函数的零点,交集及其运算,函数单调性的性质
专题:计算题,函数的性质及应用,集合
分析:(1)代入求得f(1)=-a-1,g(1)=a+b;从而得到f(1)+g(1)+3=b-1+3=0;从而解得.
(2)化简集合A={y|y=f(x),x∈[-2,0]}=[-2a,2a+2],B={y|y=g(x),x∈[-2,0]}=[-2a-2.-2];从而解得.
(3)设存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0;讨论两个函数的正负值即可.
(2)化简集合A={y|y=f(x),x∈[-2,0]}=[-2a,2a+2],B={y|y=g(x),x∈[-2,0]}=[-2a-2.-2];从而解得.
(3)设存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0;讨论两个函数的正负值即可.
解答:
解:(1)由题意,f(1)=-a-1,g(1)=a+b;
故f(1)+g(1)+3=b-1+3=0;
故b=-2;
(2)∵a>0,函数f(x)=ax2-x-2a的图象开口向上,
且对称轴为x=
>0;
∴函数f(x)=ax2-x-2a在[-2,0]上单调递减,
且f(-2)=2a+2,f(0)=-2a;
故集合A={y|y=f(x),x∈[-2,0]}=[-2a,2a+2],
同理,B={y|y=g(x),x∈[-2,0]}=[-2a-2.-2];
又∵A∩B≠ϕ,
∴-2a≤-2;
故a的取值范围为[1,+∞).
(3)设存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0;
当g(x)=ax-2=0时,x=
,当g(x)>0时,x>
;当g(x)<0时,0<x<
;
∵函数f(x)=ax2-x-2a的图象开口向上,且f(0)=-2a<0;
∴函数f(x)=ax2-x-2a必有一正一负两零点,不妨设x1<0<x2;
则易知只能有x2=
;
即f(
)=0,解得,a=1;
当a=1时,f(x)g(x)=(x-2)2(x+1)≥0;
综上所述,存在唯一实数a=1,使得对于任意的正数x,都有f(x)•g(x)≥0.
故f(1)+g(1)+3=b-1+3=0;
故b=-2;
(2)∵a>0,函数f(x)=ax2-x-2a的图象开口向上,
且对称轴为x=
| 1 |
| 2a |
∴函数f(x)=ax2-x-2a在[-2,0]上单调递减,
且f(-2)=2a+2,f(0)=-2a;
故集合A={y|y=f(x),x∈[-2,0]}=[-2a,2a+2],
同理,B={y|y=g(x),x∈[-2,0]}=[-2a-2.-2];
又∵A∩B≠ϕ,
∴-2a≤-2;
故a的取值范围为[1,+∞).
(3)设存在实数a,使得对于任意的正数x,都有f(x)•g(x)≥0;
当g(x)=ax-2=0时,x=
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
∵函数f(x)=ax2-x-2a的图象开口向上,且f(0)=-2a<0;
∴函数f(x)=ax2-x-2a必有一正一负两零点,不妨设x1<0<x2;
则易知只能有x2=
| 2 |
| a |
即f(
| 2 |
| a |
当a=1时,f(x)g(x)=(x-2)2(x+1)≥0;
综上所述,存在唯一实数a=1,使得对于任意的正数x,都有f(x)•g(x)≥0.
点评:本题主要基于对集合的运算、函数的基本性质和函数的零点等基础知识的考查,综合考查了抽象概括能力、推理论证能力、运算求解能力及应用意识和创新意识,考查了函数与方程思想、化归与转化思想、数形结合思想及分类与整合的思想.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
若曲线C1:x2+y2-4x=0与曲线C2:y(y-mx-x)=0有四个不同的交点,则实数m的取值范围是( )
A、(-
| ||||||||
B、(-
| ||||||||
C、[-
| ||||||||
D、(-∞,-
|
若实数x,y满足
,则z=3x+y的最小值是( )
|
| A、-4 | B、-2 | C、2 | D、6 |
已知a,b为非零实数,且a<b,则下列命题成立的是( )
| A、a2<b2 | ||||
| B、a2b<a3 | ||||
C、
| ||||
D、
|
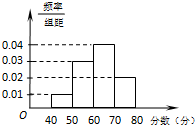 在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有
在我市2015年“创建文明城市”知识竞赛中,考评组从中抽取200份试卷进行分析,其分数的频率分布直方图如图所示,则分数在区间[60,70)上的人数大约有