题目内容
求函数y=-2tan（3x+
）的定义域、值域，并指出它的周期、奇偶性和单调性．
| π |
| 3 |
考点：正切函数的图象
专题：三角函数的图像与性质
分析：根据正切函数的图象和性质进行求解即可．
解答：
解：由3x+
≠kπ+
得x≠
+
，即函数的定义域为{x|x≠
+
}，
函数的值域为R，函数的周期T=
，
∵函数的定义域关于原点不对称，
∴函数为非奇非偶函数，
由-
+kπ＜3x+
＜
+kπ，
得-
+
＜x＜
+
，此时函数y=2tan（3x+
）为增函数，
∴函数y=-2tan（3x+
）在区间（-
+
，
+
），k∈Z上为减函数．
| π |
| 3 |
| π |
| 2 |
| kπ |
| 3 |
| π |
| 18 |
| kπ |
| 3 |
| π |
| 18 |
函数的值域为R，函数的周期T=
| π |
| 3 |
∵函数的定义域关于原点不对称，
∴函数为非奇非偶函数，
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得-
| 5π |
| 18 |
| kπ |
| 3 |
| kπ |
| 3 |
| π |
| 18 |
| π |
| 3 |
∴函数y=-2tan（3x+
| π |
| 3 |
| 5π |
| 18 |
| kπ |
| 3 |
| kπ |
| 3 |
| π |
| 18 |
点评：本题主要考查正切函数的图象和性质，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
已知a，b为非零实数，且a＜b，则下列命题成立的是（ ）
| A、a2＜b2 | ||||
| B、a2b＜a3 | ||||
C、
| ||||
D、
|
函数f（x）=1-2|x|的图象大致是（ ）
A、 |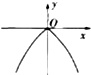
B、 |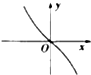
C、 |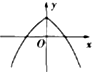
D、 |