题目内容
设椭圆的一个焦点为(
，0)，且a=2b，则椭圆的标准方程为（ ）
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：由已知可设椭圆的标准方程为
+
=1，根据a，b，c之间的关系，可得椭圆的标准方程．
| x2 |
| 4b2 |
| y2 |
| b2 |
解答：
解：∵a=2b，椭圆的一个焦点为(
，0)，
∴设椭圆的标准方程为
+
=1，
∴a2-b2=3b2=3，
故椭圆的标准方程为
+y2=1，
故选：A
| 3 |
∴设椭圆的标准方程为
| x2 |
| 4b2 |
| y2 |
| b2 |
∴a2-b2=3b2=3，
故椭圆的标准方程为
| x2 |
| 4 |
故选：A
点评：本题考查的知识点是椭圆的标准方程，椭圆的简单性质，难度不大，属于基础题．
练习册系列答案
相关题目
若A为抛物线y=
x2的顶点，过抛物线焦点的直线交抛物线于B、C两点，则
•
等于（ ）
| 1 |
| 4 |
| AB |
| AC |
| A、-3 | B、3 | C、5 | D、-5 |
命题“?x∈[-2，1]，x2-a≤0”为真命题的一个必要不充分条件是（ ）
| A、a≥4 | B、a≥1 |
| C、a≤4 | D、a≤1 |
已知正四棱锥S-ABCD中，SA=2
，那么当该棱锥的体积最大时，它的底面积为（ ）
| 3 |
| A、4 | B、8 | C、16 | D、32 |
设函数f(x)=sin(2x+
)，则下列结论正确的是（ ）
| π |
| 3 |
A、把f（x）的图象向左平移
| ||
B、f（x）的图象关于点(
| ||
C、f（x）的最小正周期为π，且在[0，
| ||
D、f（x）的图象关于直线x=-
|
已知集合A={0，1，2}，集合B={0，2，4}，则A∪B=（ ）
| A、{0} |
| B、{2} |
| C、{0，2，4} |
| D、{0，1，2，4} |
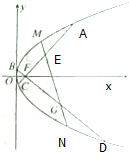如图，抛物线C：y2=2px（p＞0）的焦点F（1，0），过点F任作两条弦AC，BD，且
如图，边长为2的正方形ACDE所在平面与平面ABC垂直，AD与CE的交点为M，AC⊥BC，且AC=BC，