题目内容
已知数列{an}各项为正,Sn为其前n项和,满足2Sn=3an-3,数列{bn}为等差数列,且b2=2,b10=10,求数列{an+bn}的前n项和Tn= .
考点:数列的求和
专题:等差数列与等比数列
分析:由数列递推式求得数列{an}为等比数列并求得首项和公比,得到通项公式;由已知求出等差数列的公差,得到等差数列的通项公式,然后分组求和得答案.
解答:
解:由2Sn=3an-3,取n=1得,2S1=2a1=3a1-3,即a1=3.
当n≥2时,有2Sn-1=3an-1-3,则2an=3an-3an-1,an=3an-1(n≥2),
∴数列{an}是以3为首项,以3为公比的等比数列,
则an=3n.
在等差数列{bn}中,由b2=2,b10=10,得d=
=
=1.
∴bn=b2+(n-2)d=2+n-2=n.
∴数列{an+bn}的前n项和Tn=(31+22+…+3n)+(1+2+…+n)
=
+
=
+
=
.
故答案为:
.
当n≥2时,有2Sn-1=3an-1-3,则2an=3an-3an-1,an=3an-1(n≥2),
∴数列{an}是以3为首项,以3为公比的等比数列,
则an=3n.
在等差数列{bn}中,由b2=2,b10=10,得d=
| b10-b2 |
| 10-2 |
| 10-2 |
| 10-2 |
∴bn=b2+(n-2)d=2+n-2=n.
∴数列{an+bn}的前n项和Tn=(31+22+…+3n)+(1+2+…+n)
=
| 3(1-3n) |
| 1-3 |
| (1+n)n |
| 2 |
| 3n+1-3 |
| 2 |
| n2+n |
| 2 |
| 3(3n-1)+n2+n |
| 2 |
故答案为:
| 3(3n-1)+n2+n |
| 2 |
点评:本题考查了等比关系的确定,考查了等差数列和等比数列的前n项和,是中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
函数y=
,y=x2,y=3x,y=log2x中,在区间(0,+∞)上单调递减的是( )
| 1 |
| x |
A、y=
| ||
| B、y=x2 | ||
| C、y=3x | ||
| D、y=log2x |
设A={1,2,3},B={x|x⊆A},则下列关系表述正确的是( )
| A、A∈B | B、A∉B |
| C、A?B | D、A⊆B |
设椭圆的一个焦点为(
,0),且a=2b,则椭圆的标准方程为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
两条异面直线AB、CD分别在两平行平面α、β上,α、β间的距离为d,若三棱锥A-BCD为正四面体,则其体积为( )
A、
| ||
B、
| ||
| C、d3 | ||
D、
|
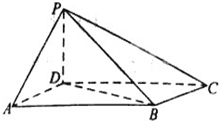 如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,且∠DAB=60°,AB=2AD=2,PD⊥底面ABC,则:
如图所示,四棱锥P-ABCD中,底面ABCD为平行四边形,且∠DAB=60°,AB=2AD=2,PD⊥底面ABC,则: