题目内容
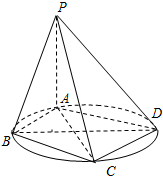 (理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=
(理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=| 3 |
(1)当AC是圆W的直径时,求证:平面PBC⊥平面PAB;
(2)当BD是圆W的直径时,求二面角A-PD-C的余弦值;
(3)在(2)的条件下,判断棱PA上是否存在一点Q,使得BQ∥平面PCD?若存在,求出AQ的长,若不存在,说明理由.
考点:与二面角有关的立体几何综合题,棱锥的结构特征,平面与平面垂直的判定
专题:计算题,证明题,存在型,空间位置关系与距离,空间角
分析:(1)应用面面垂直的判定定理,证得BC⊥平面PAB即可;
(2)过A作AK⊥平面PCD,垂足为K,过A在面PAD内,作AM⊥PD,连KD,则∠AMK为二面角A-PD-C的平面角,通过体积相等即VP-ACD=VA-PCD,求出AK,再在直角三角形PAD中求出AM,求出sin∠AMK,
从而得到cos∠AMK;
(3)假设棱PA上存在一点Q,使得BQ∥平面PCD,在面PAD内,过Q作QN∥PD,交AD于N,连接BN,由面面平行的性质定理得到BN∥CD,在直角△ABN中,求出AN,再在三角形PAD中,应用平行线分线段成比例,得到AQ,从而说明存在.
(2)过A作AK⊥平面PCD,垂足为K,过A在面PAD内,作AM⊥PD,连KD,则∠AMK为二面角A-PD-C的平面角,通过体积相等即VP-ACD=VA-PCD,求出AK,再在直角三角形PAD中求出AM,求出sin∠AMK,
从而得到cos∠AMK;
(3)假设棱PA上存在一点Q,使得BQ∥平面PCD,在面PAD内,过Q作QN∥PD,交AD于N,连接BN,由面面平行的性质定理得到BN∥CD,在直角△ABN中,求出AN,再在三角形PAD中,应用平行线分线段成比例,得到AQ,从而说明存在.
解答:
 (1)证明:∵AC是圆的直径,∴AB⊥CB,
(1)证明:∵AC是圆的直径,∴AB⊥CB,
∵PA⊥平面ABCD,∴PA⊥BC,
∴BC⊥平面PAB,
又BC?平面PBC,
∴平面PBC⊥平面PAB;
(2)解:过A作AK⊥平面PCD,垂足为K,
过A在面PAD内,作AM⊥PD,连KD,
则KD⊥PD,故∠AMK为二面角A-PD-C的平面角,
在直角三角形PAD中,PA=2,AD=
,PD=
,
AM=
,
设AK=d,则VP-ACD=VA-PCD,
PA•
•AD•S△ACD=
AK•S△PCD,
∵PA=BD=2,AD=CD=
,BD是圆W的直径,
∴△ABD为直角三角形,且∠ADB=30°,
△CBD为直角三角形,且∠CDB=30°,
∴△ACD为等边三角形,S△ACD=
,
在直角三角形PAC中,PC=
=
,
∴S△PCD=
•
•
=
,
∴
•2•
=
•AK•
即AK=
,
又AM=
,sin∠AMK=
=
,
∴cos∠AMK=
;
(3)解:在(2)的条件下,假设棱PA上存在一点Q,使得BQ∥平面PCD,
在面PAD内,过Q作QN∥PD,交AD于N,连接BN,则QN∥平面PCD,
∴平面QBN∥平面PCD,BN∥CD,
∴在直角△ABN中,∠ANB=60°,AN=
,
∴在三角形PAD中,
=
=
,
∴AQ=
.
∴在(2)的条件下,棱PA上存在一点Q,使得BQ∥平面PCD,且AQ=
.
 (1)证明:∵AC是圆的直径,∴AB⊥CB,
(1)证明:∵AC是圆的直径,∴AB⊥CB,∵PA⊥平面ABCD,∴PA⊥BC,
∴BC⊥平面PAB,
又BC?平面PBC,
∴平面PBC⊥平面PAB;
(2)解:过A作AK⊥平面PCD,垂足为K,
过A在面PAD内,作AM⊥PD,连KD,
则KD⊥PD,故∠AMK为二面角A-PD-C的平面角,
在直角三角形PAD中,PA=2,AD=
| 3 |
| 7 |
AM=
2
| ||
|
设AK=d,则VP-ACD=VA-PCD,
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∵PA=BD=2,AD=CD=
| 3 |
∴△ABD为直角三角形,且∠ADB=30°,
△CBD为直角三角形,且∠CDB=30°,
∴△ACD为等边三角形,S△ACD=
3
| ||
| 4 |
在直角三角形PAC中,PC=
| 4+3 |
| 7 |
∴S△PCD=
| 1 |
| 2 |
| 3 |
7-
|
5
| ||
| 4 |
∴
| 1 |
| 3 |
3
| ||
| 4 |
| 1 |
| 3 |
5
| ||
| 4 |
| 6 |
| 5 |
又AM=
2
| ||
|
| ||||||
|
| ||
| 5 |
∴cos∠AMK=
| 2 |
| 5 |
(3)解:在(2)的条件下,假设棱PA上存在一点Q,使得BQ∥平面PCD,
在面PAD内,过Q作QN∥PD,交AD于N,连接BN,则QN∥平面PCD,
∴平面QBN∥平面PCD,BN∥CD,
∴在直角△ABN中,∠ANB=60°,AN=
| ||
| 3 |
∴在三角形PAD中,
| AQ |
| AP |
| AN |
| AD |
| 1 |
| 3 |
∴AQ=
| 2 |
| 3 |
∴在(2)的条件下,棱PA上存在一点Q,使得BQ∥平面PCD,且AQ=
| 2 |
| 3 |
点评:本题主要考查空间直线与平面的位置关系,考查面面平行、垂直的判定与性质,同时考查空间二面角的平面角的求法,是一道综合题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
命题p:若a,b∈R,则|a|+|b|>1是|a+b|>1的充分不必要条件;命题q:函数y=
的定义域是(-∞,1],则( )
log
|
| A、“p或q”为假 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p假q真 |