题目内容
在平面直角坐标系xOy中,已知椭圆的焦点在x轴上,离心率为
,且经过点(0,2).
(1)求椭圆的标准方程;
(2)以椭圆的长轴为直径作圆O,设T为圆O上不在坐标轴上的任意一点,M为x轴上一点,过圆心O作直线TM的垂线交椭圆右准线于点Q.问:直线TQ能否与圆O总相切,如果能,求出点M的坐标;如果不能,说明理由.
| ||
| 3 |
(1)求椭圆的标准方程;
(2)以椭圆的长轴为直径作圆O,设T为圆O上不在坐标轴上的任意一点,M为x轴上一点,过圆心O作直线TM的垂线交椭圆右准线于点Q.问:直线TQ能否与圆O总相切,如果能,求出点M的坐标;如果不能,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设椭圆方程为
+
=1(a>b>0),由已知条件推导出b=2,e=
=
,由此能求出椭圆的标准方程.
(2)存在点M(
,0),使得直线TQ与圆O总相切.设点T(x0,y0),M(c,0),由已知条件推导出x0y0≠0且x02+y02=9,直线OQ的方程为y=-
x,Q(
,-
),由此能推导出存在这样点M(
,0),使得TQ与圆O总相切.
| x2 |
| a2 |
| y2 |
| b2 |
| c |
| a |
| ||
| 3 |
(2)存在点M(
| 5 |
| x0-c |
| y0 |
9
| ||
| 5 |
9
| ||
| 5y0 |
| 5 |
解答:
解:(1)设椭圆方程为
+
=1(a>b>0),
∵椭圆经过点(0,2),∴b=2,
又∵离心率为
,∴e=
=
,可令c=
x,a=3x,
∴b2=a2-c2=4x2=4,解得x=1,
∴椭圆的标准方程为
+
=1.…(6分)
(2)存在点M(
,0),使得直线TQ与圆O总相切.…(7分)
设点T(x0,y0),M(c,0),
∵T在以椭圆的长轴为直径作圆O上,且不在坐标轴上的任意点,
∴x0y0≠0且x02+y02=9,又∵kTM=
,
∴OQ⊥TM,∴kOQ=-
,
∴直线OQ的方程为y=-
x,…(10分)
∵点Q在直线x=
上,
令x=
,得y=-
,
即Q(
,-
),…(12分)
∴kTQ=
=
=
,
又∵kOT=
,TQ与圆O总相切,∴OT⊥TQ,
于是有kOT•kTQ=-1,kTQ=-
,
即
=-
恒成立,解得c=
,
∴存在这样点M(
,0),使得TQ与圆O总相切.…(16分)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆经过点(0,2),∴b=2,
又∵离心率为
| ||
| 3 |
| c |
| a |
| ||
| 3 |
| 5 |
∴b2=a2-c2=4x2=4,解得x=1,
∴椭圆的标准方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)存在点M(
| 5 |
设点T(x0,y0),M(c,0),
∵T在以椭圆的长轴为直径作圆O上,且不在坐标轴上的任意点,
∴x0y0≠0且x02+y02=9,又∵kTM=
| y0 |
| x0-c |
∴OQ⊥TM,∴kOQ=-
| x0-c |
| y0 |
∴直线OQ的方程为y=-
| x0-c |
| y0 |
∵点Q在直线x=
9
| ||
| 5 |
令x=
9
| ||
| 5 |
9
| ||
| 5y0 |
即Q(
9
| ||
| 5 |
9
| ||
| 5y0 |
∴kTQ=
y0+
| ||||
x0-
|
5
| ||||
y0(5x0-9
|
5(9-x02)+9
| ||
y0(5x0-9
|
又∵kOT=
| y0 |
| x0 |
于是有kOT•kTQ=-1,kTQ=-
| ||
| y0 |
即
5(9-x02)+9
| ||
y0(5x0-9
|
| x0 |
| y0 |
| 5 |
∴存在这样点M(
| 5 |
点评:本题考查椭圆方程的求法,考查满足条件的点的判断与求法,解题时要认真审题,注意直线与椭圆的位置关系的灵活运用.

练习册系列答案
相关题目
已知i是虚数单位,若(2i-1)z=5,则复数z在复平面内对应的点的坐标为( )
| A、(-2,-1) |
| B、(2,-1) |
| C、(-1,-2) |
| D、(-1,2) |
 如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是
如图所示,AC和AB分别是圆O的切线,且OC=3,AB=4,延长AO到D点,则△ABD的面积是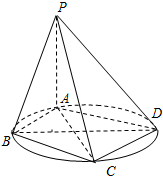 (理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=
(理)如图,四棱锥P-ABCD的底面ABCD是圆内接四边形(记此圆为W),PA⊥平面ABCD,PA=BD=2,AD=CD=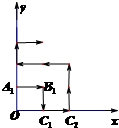 某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么
某地区为了绿化环境进行大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在点A1(0,1),第二棵树在点B1(1,1),第三棵树在点C1(1,0),第四棵树在点C2(2,0),接着按图中箭头方向每隔一个单位种一棵树,那么