题目内容

命题“?x∈[1，2]，使x+
2
x
+a≥0”是真命题，则实数a的取值范围为
 
．
考点：特称命题
专题：简易逻辑
分析：根据特称命题的定义和性质，即可得到结论．
解答： 解：若“?x∈[1，2]，使x+
2
x
+a≥0”是真命题，
则等价为“?x∈[1，2]，使a≥-（x+
2
x
）min，
设g（x）=-（x+
2
x
）≤-2
2
，
而g（1）=-3，g（2）=-3，
∴-3≤g（x）≤-2
2
，
∴a≥-3，
故答案为：a≥-3
点评：本题主要考查特称命题的应用，注意存在性命题和任意性命题的区别．
练习册系列答案
相关题目
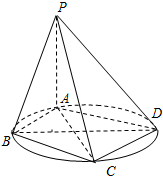（理）如图，四棱锥P-ABCD的底面ABCD是圆内接四边形（记此圆为W），PA⊥平面ABCD，PA=BD=2，AD=CD=
3
．
（1）当AC是圆W的直径时，求证：平面PBC⊥平面PAB；
（2）当BD是圆W的直径时，求二面角A-PD-C的余弦值；
（3）在（2）的条件下，判断棱PA上是否存在一点Q，使得BQ∥平面PCD？若存在，求出AQ的长，若不存在，说明理由．
已知函数f（x）=
2x，(x≤1)
x2-2x+2，(x＞1)
，若关于x的函数g（x）=f（x）-m有两个零点，则实数m的取值范围是
 
．
在数列{an}中，a1=3，点列（
an
，
an-1
）（其中n∈N*，且n＞1）在直线x-y-
3
=0上，则数列{an}的通项公式an=
 
．
若不等式组
y-x≥0
y-kx-1≤0
x≥0
表示的平面区域的面积等于抛物线y=-x2+1与x轴围成的封闭区域的面积，则k=
 
．
以平面直角坐标系的原点为极点，以x轴的正半轴为极轴，建立极坐标系，则圆x2+y2=2上的点到曲线ρcosθ+ρsinθ=4（ρ，θ∈R）的最短距离是
 
．
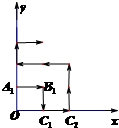某地区为了绿化环境进行大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在点A1（0，1），第二棵树在点B1（1，1），第三棵树在点C1（1，0），第四棵树在点C2（2，0），接着按图中箭头方向每隔一个单位种一棵树，那么
（1）第n棵树所在点坐标是（3，1），则n=
 
；
（2）第2014棵树所在点的坐标是
 
．
已知函数f（x）=ax3+bx2+cx+d（a≠0）的对称中心为M（x0，y0），记函数f（x）的导函数为f′（x），f′（x）的导函数为f″（x），则有f″（x0）=0．若函数f（x）=x3-3x2，则可求得：f（
1
4
）+f（
2
4
）+f（
3
4
）+f（
4
4
）+f（
5
4
）+f（
6
4
）+f（
7
4
）=
 
．
已知a，b，c为△ABC的三边，若b2+c2-a2=bc，则
b+c
a
的取值范围是（　　）
A、（1，2]
B、（1，
3
]
C、[
3
，2]
D、（
3
，2]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网