题目内容
若满足条件
的点P（x，y）构成三角形区域，则实数k的取值范围是 ．
|
考点：简单线性规划
专题：不等式的解法及应用
分析：作出不等式组对应的平面区域，根据平面区域是三角形，即可确定k的取值范围．
解答：
解：作出不等式组
对应的平面区域
直线kx-y-2k+1=0得k（x-2）+1-y=0，则直线过定点（2，1），
当直线k（x-2）+1-y=0与x+y-2=0平行时，即k=-1时，此时对应的平面区域不是三角形，
∴要使对应的平面区域是三角形，
则k（x-2）+1-y=0与x+y-2=0在第一象限内相交，即k＜-1，
故答案为：（-∞，-1）．
|
直线kx-y-2k+1=0得k（x-2）+1-y=0，则直线过定点（2，1），
当直线k（x-2）+1-y=0与x+y-2=0平行时，即k=-1时，此时对应的平面区域不是三角形，
∴要使对应的平面区域是三角形，
则k（x-2）+1-y=0与x+y-2=0在第一象限内相交，即k＜-1，
故答案为：（-∞，-1）．
点评：本题主要考查线性规划的应用，利用数形结合是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
执行如图所示的程序框图，输出的S值为（ ）
| A、2 | B、-2 | C、4 | D、-4 |
已知幂函数y=f（x）的图象过点（
，
），则f（4）的值为（ ）
| 1 |
| 3 |
| ||
| 3 |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
如图所示，AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是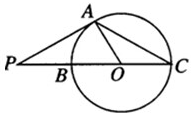
如图，已知P是圆O外一点，PA为圆O的切线，A为切点．割线PBC经过圆心O，若PA=3
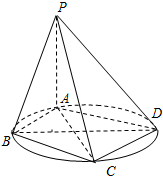（理）如图，四棱锥P-ABCD的底面ABCD是圆内接四边形（记此圆为W），PA⊥平面ABCD，PA=BD=2，AD=CD=