题目内容
已知椭圆E：
+
=1与直线l：y=kx+m交于A，B两点，O为坐标原点．
（Ⅰ）若直线l经过椭圆E的左焦点，且k=1，求△AOB的面积；
（Ⅱ）若OA⊥OB，且直线l与圆O：x2+y2=r2相切，求圆O的半径r的值．
| x2 |
| 8 |
| y2 |
| 4 |
（Ⅰ）若直线l经过椭圆E的左焦点，且k=1，求△AOB的面积；
（Ⅱ）若OA⊥OB，且直线l与圆O：x2+y2=r2相切，求圆O的半径r的值．
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：（Ⅰ）若直线l经过椭圆E的左焦点，且k=1，可得直线的方程，代入椭圆E：
+
=1，求出交点坐标，即可求△AOB的面积；
（Ⅱ）直线l的方程与椭圆方程联立即可得到根与系数的关系，再利用OA⊥OB，可得x1x2+y1y2=0，从而可得3m2=8（1+k2），利用点到直线的距离公式即可得出．
| x2 |
| 8 |
| y2 |
| 4 |
（Ⅱ）直线l的方程与椭圆方程联立即可得到根与系数的关系，再利用OA⊥OB，可得x1x2+y1y2=0，从而可得3m2=8（1+k2），利用点到直线的距离公式即可得出．
解答：
解：（Ⅰ）椭圆E的左焦点为（-2，0），k=1，代入y=kx+m，可得m=2
∴直线l：y=x+2
代入椭圆E：
+
=1，整理可得3x2+8x=0，
∴x=0或x=-
，
∴y=2或y=-
，
∴△AOB的面积S=
•2•(2+
)=
；
（Ⅱ）设A（x1，y1），B（x2，y2）．
直线l：y=kx+m，代入椭圆E：
+
=1，消去y得到（1+2k2）x2+4kmx+2m2-8=0．
∴x1+x2=-
，x1x2=
（*）
∵OA⊥OB，
∴x1x2+y1y2=0．
又y1y2=（kx1+m）（kx2+m），
∴（1+k2）x1x2+km（x1+x2）+m2=0．
把（*）代入可得3m2=8（1+k2），
∵直线l与圆O：x2+y2=r2相切，
∴∴点O到直线l的距离d=r=
=
．
∴直线l：y=x+2
代入椭圆E：
| x2 |
| 8 |
| y2 |
| 4 |
∴x=0或x=-
| 8 |
| 3 |
∴y=2或y=-
| 2 |
| 3 |
∴△AOB的面积S=
| 1 |
| 2 |
| 2 |
| 3 |
| 8 |
| 3 |
（Ⅱ）设A（x1，y1），B（x2，y2）．
直线l：y=kx+m，代入椭圆E：
| x2 |
| 8 |
| y2 |
| 4 |
∴x1+x2=-
| 4km |
| 1+2k2 |
| 2m2-8 |
| 1+2k2 |
∵OA⊥OB，
∴x1x2+y1y2=0．
又y1y2=（kx1+m）（kx2+m），
∴（1+k2）x1x2+km（x1+x2）+m2=0．
把（*）代入可得3m2=8（1+k2），
∵直线l与圆O：x2+y2=r2相切，
∴∴点O到直线l的距离d=r=
| |m| | ||
|
2
| ||
| 3 |
点评：本题综合考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到根与系数的关系、向量垂直与数量积得关系、点到直线的距离公式等基础知识与基本技能，考查了推理能力和计算能力．
练习册系列答案
相关题目
已知x，y满足不等式组
，则
的取值范围是（ ）
|
| 2y+x |
| x |
| A、[1，4] |
| B、[2e+1，9] |
| C、[3，2e+1] |
| D、[1，e] |
如图所示，AC和AB分别是圆O的切线，且OC=3，AB=4，延长AO到D点，则△ABD的面积是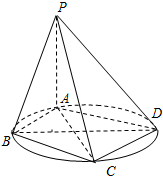
（理）如图，四棱锥P-ABCD的底面ABCD是圆内接四边形（记此圆为W），PA⊥平面ABCD，PA=BD=2，AD=CD=