题目内容
已知数列{an}满足an+1=6an+2n+1,a1=1.
(1)求证:数列{
+
}是等比数列;
(2)若数列{an+r2n}是等比数列,求r;
(3)求
.
(1)求证:数列{
| an |
| 2n |
| 1 |
| 2 |
(2)若数列{an+r2n}是等比数列,求r;
(3)求
| an |
| 2 |
考点:等比关系的确定
专题:计算题,等差数列与等比数列
分析:(1)可对等式两边同除以2n+1,再由等比数列的定义,即可得证;
(2)可由等比数列的性质,得到r的方程,解出,再加以检验即可;
(3)由(1)得到an,即可得到所求.
(2)可由等比数列的性质,得到r的方程,解出,再加以检验即可;
(3)由(1)得到an,即可得到所求.
解答:
(1)证明:数列{an}满足an+1=6an+2n+1,a1=1,
令bn=
+
,则bn+1=
+
,
则有
+
=3(
+
),即有bn+1=3bn,
故数列{
+
}是首项为1,公比为3的等比数列;
(2)解:由(1)得,
+
=3n-1,
即有an=2n(3n-1-
),
若数列{an+r2n}是等比数列,
即有a1+2r,a2+4r,a3+8r成等比数列,
即1+2r,10+4r,68+8r成等比数列,
则(1+2r)(68+8r)=(10+4r)2,
解得r=
,
则an+r2n=2n(3n-1-
)+
•2n=
•6n,
则{an+r2n}是以2为首项,6为公比的等比数列;
(3)解:由(2)得,
=2n-1(3n-1-
)=6n-1-2n-2.
令bn=
| an |
| 2n |
| 1 |
| 2 |
| an+1 |
| 2n+1 |
| 1 |
| 2 |
则有
| an+1 |
| 2n+1 |
| 1 |
| 2 |
| an |
| 2n |
| 1 |
| 2 |
故数列{
| an |
| 2n |
| 1 |
| 2 |
(2)解:由(1)得,
| an |
| 2n |
| 1 |
| 2 |
即有an=2n(3n-1-
| 1 |
| 2 |
若数列{an+r2n}是等比数列,
即有a1+2r,a2+4r,a3+8r成等比数列,
即1+2r,10+4r,68+8r成等比数列,
则(1+2r)(68+8r)=(10+4r)2,
解得r=
| 1 |
| 2 |
则an+r2n=2n(3n-1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
则{an+r2n}是以2为首项,6为公比的等比数列;
(3)解:由(2)得,
| an |
| 2 |
| 1 |
| 2 |
点评:本题考查等比数列的判断,注意运用定义,考查等比数列的性质,考查构造数列的思想方法求复杂数列的通项的方法,考查运算能力,属于中档题.

练习册系列答案
相关题目
已知f(x)=2x+3(x∈R),若|f(x)|<a的必要条件是|x+1|<b(a,b>0),则a,b之间的关系是( )
A、b≥
| ||
B、b<
| ||
C、a≤
| ||
D、a>
|
函数f(x)=x2-
x+
,x∈[0,1],n∈Z的值域中恰好有一个整数,则n的值为( )
| n |
| 2 |
| 1 |
| 2 |
| A、0或1 |
| B、0或2 |
| C、0或1或3或4 |
| D、0或1或2或3 |
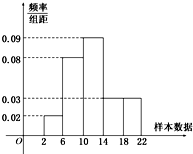 如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.
如图是学校从走读生中随机调查200名走读生早上上学所需时间(单位:分钟)样本的频率分布直方图.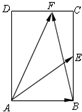 如图,在矩形ABCD中,AB=2,BC=2
如图,在矩形ABCD中,AB=2,BC=2