题目内容
11.已知等比数列{an}的公比为q,前n项和为Sn,若点(n,Sn)在函数y=2n+1+m的图象上,则m=-2.分析 点(n,Sn)在函数y=2n+1+m的图象上,可得:Sn=2n+1+m,分别解得a1,a2,a3,利用等比数列的性质即可得出.
解答 解:∵点(n,Sn)在函数y=2n+1+m的图象上,
∴Sn=2n+1+m,
∴a1=4+m,a2=4,a3=8,
∵数列{an}是等比数列,
∴42=8×(4+m),解得m=-2.
故答案为:-2.
点评 本题考查了递推关系、等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.方程$\frac{{x}^{2}}{4-t}$+$\frac{{y}^{2}}{t-1}$=1表示椭圆,则t的取值范围是( )
| A. | 1<t<4 | B. | t<1或t>4 | C. | t>4 | D. | 1<t<$\frac{5}{2}$或$\frac{5}{2}$<t<4 |
6.计算${∫}_{0}^{4}$$\sqrt{16-{x}^{2}}dx$等于( )
| A. | 8π | B. | 16π | C. | 4π | D. | 32π |
14.复数$\frac{2+i}{1-i}$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
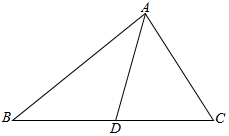 如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.
如图,在△ABC中,∠C=60°,D是BC上一点,AB=31,BD=20,AD=21.