题目内容
设三个正实数a、b、c，若存在x∈（-1，1），使得a2=b2+c2-2bcx成立，试问以a、b、c为三边的长是否可以构成三角形？请说明理由．
考点：余弦定理
专题：解三角形
分析：由条件可得x=
，根据余弦定理可得x=cosA．再根据A∈（0，π），可得 x∈（-1，1）．故以a、b、c为三边的长，可以构成三角形．
| b2+c2-a2 |
| 2bc |
解答：
解：由a2=b2+c2-2bcx，可得 x=
，∴x=cosA．
再根据A∈（0，π），可得 x∈（-1，1）．
故以a、b、c为三边的长，可以构成三角形．
| b2+c2-a2 |
| 2bc |
再根据A∈（0，π），可得 x∈（-1，1）．
故以a、b、c为三边的长，可以构成三角形．
点评：本题主要考查余弦定理，余弦函数的定义域和值域，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知
+
＞1+2m（x＞0，y＞0）恒成立，则实数m的取值范围是（ ）
| 2y |
| x |
| 8x |
| y |
A、m＞
| ||
B、m＜
| ||
| C、m＜2 | ||
| D、m＞2 |
设函数f（x）的导函数为f′（x），对任意x∈R，都有xf′（x）＞f（x）成立，则（ ）
| A、3f（2）＞2f（3） |
| B、3f（2）=2f（3） |
| C、3f（2）＜2f（3） |
| D、3f（2）与2f（3）的大小不确定 |
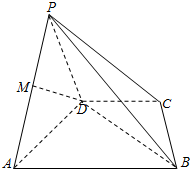如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．
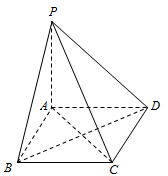如图，棱锥P-ABCD的底面ABCD是矩形，PA⊥平面ABCD，PA=AD=2，BD=2