题目内容
某单位建造一间背面靠墙的仓库，已知仓库地面面积为27平方米，仓库正面每平方米的造价为1500元，仓库侧面每平方米的造价为1000元，仓库顶的造价为6400元，如果墙高3米，且不计房屋背面和地面的费用，问怎样设计总造价最低？最低造价是多少？
考点：基本不等式在最值问题中的应用
专题：应用题,不等式的解法及应用
分析：设底面的长为xm，宽ym，则y=
m．设房屋总造价为f（x），由题意可得f（x）=3x•1500+3×
×1000×2+6400，利用基本不等式即可得出．
| 27 |
| x |
| 27 |
| x |
解答：
解：如图所示，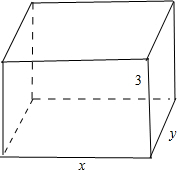
设底面的长为xm，宽ym，则y=
m．
设房屋总造价为f（x），
由题意可得f（x）=3x•1500+3×
×1000×2+6400
=4500x+
×1000+6400≥2
=2700
当且仅当4500x+
×1000，即x=6时取等号．
答：当底面的长宽分别为6m，4.5m时，可使房屋总造价最低，总造价是2700
元．
设底面的长为xm，宽ym，则y=| 27 |
| x |
设房屋总造价为f（x），
由题意可得f（x）=3x•1500+3×
| 27 |
| x |
=4500x+
| 27×6 |
| x |
4500x•
|
| 10 |
当且仅当4500x+
| 27×6 |
| x |
答：当底面的长宽分别为6m，4.5m时，可使房屋总造价最低，总造价是2700
| 10 |
点评：本题考查的知识点是函数模型的选择与应用，函数的值域，其中根据已知条件构造房屋总造价的函数解析式，将实际问题转化为函数的最值问题是解答本题的关键．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
某班级组织学生参加英语测试，成绩的频率分布直方图如图所示，若低于60分的人数是15人，则该班的学生人数是（ ）| A、45 | B、50 | C、55 | D、60 |
下列说法不正确的是（ ）
| A、一个命题与它的逆命题、否命题、逆否命题等四种命题中真命题个数为偶数 | ||||||||
| B、命题：“若xy=0，则x=0或y=0”的逆否命题是“若x≠0或y≠0，则xy≠0” | ||||||||
C、椭圆
| ||||||||
D、已知两条直线l1：ax+3y-1=0，l2：x+by+1=0，则l1⊥l2的充分不必要条件是
|