题目内容

从1～10十个整数中一次取出4个数，并由小到大排列，以ξ表示这4个数中的第二个，求ξ的分布列．
考点：离散型随机变量及其分布列
专题：计算题,概率与统计
分析：由题意，ξ=2，3，4，5，6，7，8，求出相应的概率，可得ξ的分布列．
解答： 解：由题意，ξ=2，3，4，5，6，7，8，则
P（ξ=2）=
C
2
8
C
4
10
=
2
15
，P（ξ=3）=
C
1
2
C
2
7
C
4
10
=
1
5
，P（ξ=4）
C
1
3
C
2
6
C
4
10
=
3
14
，P（ξ=5）=
C
1
4
C
2
5
C
4
10
=
4
21
，
P（ξ=6）=
C
1
5
C
2
4
C
4
10
=
1
7
，P（ξ=7）=
C
1
6
C
2
3
C
4
10
=
3
35
，P（ξ=8）=
C
1
7
C
4
10
=
1
30
，
∴ξ的分布列
 ξ  2  3  4  5  6  7  8
 P  
2
15
  
1
5
  
3
14
  
4
21
  
1
7
  
3
35
  
1
30
点评：本题考查离散型随机变量及其分布列，确定变量的取值，求出相应的概率是关键．
练习册系列答案
相关题目
数列-3，7，-11，15，…的一个通项公式是（　　）
A、an=（-1）n（4n-1）
B、an=（-1）n（4n+1）
C、an=4n-7
D、an=（-1）n+1（4n-1）
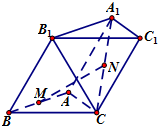两个不同的口袋中，各装有大小、形状完全相同的1个红球、2个黄球．现从每一个口袋中各任取2球，设随机变量ξ为取得红球的个数，则Eξ=
 
．
设三个正实数a、b、c，若存在x∈（-1，1），使得a2=b2+c2-2bcx成立，试问以a、b、c为三边的长是否可以构成三角形？请说明理由．
如图，已知三棱柱ABC-A1B1C1，侧面BCC1B1⊥底面ABC．
（Ⅰ）若M、N分别为AB、A1C的中点，求证：MN∥平面BCC1B1；
（Ⅱ）若三棱柱ABC-A1B1C1的各棱长均为2，侧棱BB1与底面ABC所成的角为
60°．问在线段CC1上是否存在一点P，使得平面ABP与底面ABC的所成角为
60°，若存在，求BP的长度，若不存在，说明理由．
为调查我校高一高二两个年级学生是否支持某项课外运动，用简单随机抽样方法从我校调查了500位同学，结果如下：
  高一年级 高二年级
不支持 30 40
支持 160 270
（Ⅰ）估计我校高一高二两个年级学生中，支持该项课外活动同学的比例；
（Ⅱ）能否可以认为我校高一高二两个年级学生是否支持该项课外活动与同学所在年级有关？（参考公式及相关数据见本题下方）
（Ⅲ）根据（Ⅱ）的结论，指明是否需要采用分层抽样的调查方法来估计我校高一高二两个年级学生中支持该项课外活动的比例？
附：X2=
n(n11n22-n12n21)2
n1+n2+n+1n+2
     
P（x2≥k） 0.050 0.030  0.001 
k  3.041  6.635  10.828
经计算得：n1+n2+n+1n+2=1.77×109．
在△ABC中，AB=2，∠C=45°，求△ABC的面积的最大值．
如图，已知三棱柱ABC-A1B1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，M是CC1的中点，N是BC的中点，点P在直线A1B1上，且满足
A1P
=λ
A1B
．
（Ⅰ）当λ=
1
2
时，求直线PN与平面ABC所成的角θ的正弦值；
（Ⅱ）若平面PMN与平面ABC所成的角为45°，试确定点P的位置．
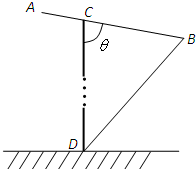某运输装置如图所示，其中钢结构ABD是AB=BD=l，∠B=
π
3
的固定装置，AB上可滑动的点C使CD垂直与底面（C不A，B与重合），且CD可伸缩（当CD伸缩时，装置ABD随之绕D在同一平面内旋转），利用该运输装置可以将货物从地面D处沿D→C→A运送至A处，货物从D处至C处运行速度为v，从C处至A处运行速度为3v．为了使运送货物的时间t最短，需在运送前调整运输装置中∠DCB=θ的大小．
（1）当θ变化时，试将货物运行的时间t表示成θ的函数（用含有v和l的式子）；
（2）当t最小时，C点应设计在AB的什么位置？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网