题目内容
已知函数f(x)=-x2+ax-b
(1)若a,b都是从0,1,2,3,4五个数中任取一个数,求上述函数有零点的概率;
(2)若a,b都是从区间[0,4]上任取得一个数,求f(1)>0得概率;
(3)设有关于x的一元二次方程3ax+b2-b-f(x)=0,若a是从区间[0,3]内任取得一个数,b是从区间[0,2]内任取一个数,求上述方程有实数根的概率.
(1)若a,b都是从0,1,2,3,4五个数中任取一个数,求上述函数有零点的概率;
(2)若a,b都是从区间[0,4]上任取得一个数,求f(1)>0得概率;
(3)设有关于x的一元二次方程3ax+b2-b-f(x)=0,若a是从区间[0,3]内任取得一个数,b是从区间[0,2]内任取一个数,求上述方程有实数根的概率.
考点:几何概型,古典概型及其概率计算公式
专题:应用题,概率与统计
分析:(1)本题是一个古典概型,试验发生包含的事件a,b都从0,1,2,3,4五个数中任取的一个数的基本事件总数为5×5个,函数有零点的条件为△=a2-4b≥0,即a2≥4b,列举出所有事件的结果数,得到概率.
(2)由题意知本题是一个几何概型,试验发生包含的事件可以写出a,b满足的条件,满足条件的事件也可以写出,画出图形,做出两个事件对应的图形的面积,得到比值.
(3)由题意求出点(a,b)所构成的矩形面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率.
(2)由题意知本题是一个几何概型,试验发生包含的事件可以写出a,b满足的条件,满足条件的事件也可以写出,画出图形,做出两个事件对应的图形的面积,得到比值.
(3)由题意求出点(a,b)所构成的矩形面积,再由线性规划知识求出满足a≥b的区域面积,由测度比是面积比求概率.
解答:
解:(1)由题意知本题是一个古典概型,
试验发生包含的事件a,b都从0,1,2,3,4五个数中任取的一个数的
基本事件总数为N=5×5=25个
函数有零点的条件为△=a2-4b≥0,即a2≥4b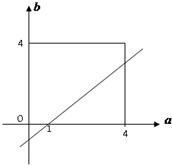
∵事件“a2≥4b”包含:(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(3,2),(4,0),(4,1),(4,2),(4,3),(4,4)
∴事件“a2≥4b”的概率为p=
;
(2)f(1)=-1+a-b>0,∴a-b>1
则a,b都是从区间[0,4]任取的一个数,有f(1)>0,
即满足条件:
转化为几何概率如图所示,
∴事件“f(1)>0”的概率为
=
;
(3)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.
如图,所求的概率
=
.
试验发生包含的事件a,b都从0,1,2,3,4五个数中任取的一个数的
基本事件总数为N=5×5=25个
函数有零点的条件为△=a2-4b≥0,即a2≥4b

∵事件“a2≥4b”包含:(0,0),(1,0),(2,0),(2,1),(3,0),(3,1),(3,2),(4,0),(4,1),(4,2),(4,3),(4,4)
∴事件“a2≥4b”的概率为p=
| 12 |
| 25 |
(2)f(1)=-1+a-b>0,∴a-b>1
则a,b都是从区间[0,4]任取的一个数,有f(1)>0,
即满足条件:
|

∴事件“f(1)>0”的概率为
| ||
| 4×4 |
| 9 |
| 32 |
(3)试验的全部结果所构成的区域为{(a,b)|0≤a≤3,0≤b≤2}.
构成事件A的区域为{(a,b)|0≤a≤3,0≤b≤2,a≥b}.
如图,所求的概率
3×2-
| ||
| 3×2 |
| 2 |
| 3 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
下列各函数中,其图象经过点(1,0)的是( )
| A、y=x2+1 | ||
B、y=
| ||
| C、y=3x | ||
| D、y=log2x |
下面说法正确的是( )
| A、命题“?x∈R,使得x2+x+1≥0”的否定是“?x∈R,使得x2+x+1≥0” |
| B、实数x>y是x2>y2成立的充要条件 |
| C、设p,q为简单命题,若“p∨q”为假命题,则“¬p∧¬q”也为假命题 |
| D、命题“若cosα≠1,则α≠0”的逆否命题为真命题 |