题目内容
已知两定点M(-1,0),N(1,0),若直线上存在点P,使得|PM|+|PN|=4,则称该直线为“A型直线”,给出下列直线:①y=x+1;②y=2;③y=-x+3;④y=-2x+3,其中是“A型直线”的有 .
考点:直线与圆锥曲线的关系,命题的真假判断与应用
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:运用椭圆的定义可得,点P的轨迹方程是
+
=1,把①,②,③,④分别和
+
=1,联立方程组,如果方程组有解,则这条直线就是“A型直线”.
由判别式大于0,即可判断①;代入y=2,无解,即可判断②;
由判别式小于0,即可判断③;由判别式大于0,即可判断④.
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
由判别式大于0,即可判断①;代入y=2,无解,即可判断②;
由判别式小于0,即可判断③;由判别式大于0,即可判断④.
解答:
解:由椭圆的定义可知,点P的轨迹是以M,N为焦点的椭圆,其方程是
+
=1,
对于①,把y=x+1代入
+
=1,并整理得7x2+8x-8=0,由△=82-4×7×(-8)>0,
则y=x+1是“A型直线”;
对于②,把y=2代入
+
=1,得
=-
不成立,∴y=2不是“A型直线”;
对于③,把y=-x+3代入
+
=1,并整理得,7x2-24x+24=0,△=(-24)2-4×7×24<0,
则y=-x+3不是“A型直线”;
对于④把y=-2x+3代入
+
=1,并整理得,19x2-48x+24=0,由△=(-48)2-4×19×24>0,
则y=-2x+3是“A型直线”.
故答案为:①④.
| x2 |
| 4 |
| y2 |
| 3 |
对于①,把y=x+1代入
| x2 |
| 4 |
| y2 |
| 3 |
则y=x+1是“A型直线”;
对于②,把y=2代入
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| 1 |
| 3 |
对于③,把y=-x+3代入
| x2 |
| 4 |
| y2 |
| 3 |
则y=-x+3不是“A型直线”;
对于④把y=-2x+3代入
| x2 |
| 4 |
| y2 |
| 3 |
则y=-2x+3是“A型直线”.
故答案为:①④.
点评:本题是新定义题,考查了椭圆的定义及标准方程,考查了数学转化思想方法及方程思想方法,解答此题的关键是把问题转化为判断直线方程与椭圆方程联立的方程组是否有解,属中档题.

练习册系列答案
相关题目
在空间直角坐标系O-xyz中,点B是点A(1,2,3)在坐标平面yOz内的射影,则|OB|等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知向量
=(3,2),
=(-1,2),
=(4,1),若
+k
与2
-
共线,则k的值是( )
| a |
| b |
| c |
| a |
| c |
| b |
| a |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
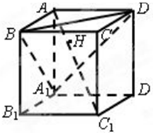 如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题:
如图,正方体AC1的棱长为1,连结AC1,交平面A1BD于H,有以下四个命题: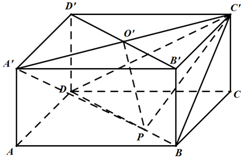 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).



