题目内容
在平面直角坐标系中,曲线C的方程为
(θ为参数),在以此坐标系的原点为极点,x轴的正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin(θ+
)=1,则直线l与曲线C的公共点共有 个.
|
| π |
| 4 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:直线与圆
分析:由曲线C的方程
(θ为参数),消去参数化为x2+y2=1,可得圆心C,半径r.由直线l的极坐标方程ρsin(θ+
)=1,展开为
(ρsinθ+ρcosθ)=1,化为y+x-
=0.再利用点到直线的距离公式可得圆心到直线l的距离d,再与半径r比较大小即可.
|
| π |
| 4 |
| ||
| 2 |
| 2 |
解答:
解:由曲线C的方程
(θ为参数),消去参数化为x2+y2=1,可得圆心C(0,0),半径r=1.
由直线l的极坐标方程ρsin(θ+
)=1,展开为
(ρsinθ+ρcosθ)=1,化为y+x-
=0.
∴圆心C到直线l的距离d=
=1=r.
因此直线l与⊙C相切,有且只有一个公共点.
故答案为:1.
|
由直线l的极坐标方程ρsin(θ+
| π |
| 4 |
| ||
| 2 |
| 2 |
∴圆心C到直线l的距离d=
| ||
|
因此直线l与⊙C相切,有且只有一个公共点.
故答案为:1.
点评:本题考查了把极坐标方程化为直角坐标方程、参数方程化为普通方程、直线与曲线的交点判断、点到直线的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
向量
=(1,2),
=(-2,6),则
•
等于( )
| a |
| b |
| a |
| b |
| A、4 | B、6 | C、8 | D、10 |
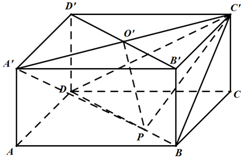 如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).
如图,在长方体ABCD-A′B′C′D′中,DA=DC=2,DD′=1,A′C′与B′D′相交于点O′,点P在线段BD上(点P与点B不重合).




 如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.
如图,在矩形ABCD中,AB=4,BC=3,沿对角线BD将Rt△ABD折起,使点A到P点,且点P在平面BCD内的射影O恰好落在CD边上,求二面角P-BD-C的正弦值.