题目内容
若
:
:C
=3:5:5,则m,n的值分别是( )
| C | m n+2 |
| C | m+1 n+2 |
m+2 n+2 |
| A、m=5,n=2 |
| B、m=5,n=5 |
| C、m=2,n=5 |
| D、m=4,n=4 |
考点:组合及组合数公式
专题:计算题
分析:由题意可得
=
,即 n+2=m+1+m+2,解得 n=2m+1.再根据
:
=3:5 利用组合数公式化简可得
=
,解得m的值,可得n=2m+1的值
| C | m+1 n+2 |
| C | m+2 n+2 |
| C | m n+2 |
| C | m+1 n+2 |
| m+1 |
| m+3 |
| 3 |
| 5 |
解答:
解:若
:
:C
=3:5:5,
则有
=
,
∴n+2=m+1+m+2,
解得 n=2m+1.
再根据
:
=3:5,
可得
:
=3:5,
即
:
=3:5,
即
=
,
解得 m=2,
∴n=2m+1=5,
故选:C.
| C | m n+2 |
| C | m+1 n+2 |
m+2 n+2 |
则有
| C | m+1 n+2 |
| C | m+2 n+2 |
∴n+2=m+1+m+2,
解得 n=2m+1.
再根据
| C | m n+2 |
| C | m+1 n+2 |
可得
| C | m 2m+3 |
| C | m+1 2m+3 |
即
| (2m+3)! |
| m!•(m+3)! |
| (2m+3)! |
| (m+1)!•(m+2)! |
即
| m+1 |
| m+3 |
| 3 |
| 5 |
解得 m=2,
∴n=2m+1=5,
故选:C.
点评:本题主要考查组合数的计算公式、组合数的性质应用,属于基础题.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
若P=
sinxdx,Q=
(-cosx)dx,R=
dx,则P,Q,R的大小关系是( )
| ∫ | π
|
| ∫ | π
|
| ∫ | π
|
| 1 |
| x |
| A、P=Q>R |
| B、P=Q<R |
| C、P>Q>R |
| D、P<Q<R |
下列各数85(9)、1000(4)、111111(2)中最小的数是( )
| A、85(9) |
| B、111111(2) |
| C、1000(4) |
| D、不确定 |
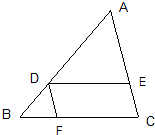 (几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=
(几何证明选讲选做题)如图,在△ABC中,DE∥BC,DF∥AC,AE=4,EC=2,BC=8,则BF=