题目内容
已知函数f(x)=ax2+bcosx+sinx-1满足f(
)=5,则f(-
)的值是 .
| π |
| 6 |
| π |
| 6 |
考点:函数奇偶性的性质,函数的值
专题:函数的性质及应用
分析:根据条件f(
)=5,直接建立方程即可求解.
| π |
| 6 |
解答:
解:∵函数f(x)=ax2+bcosx+sinx-1,且f(
)=5,
∴f(
)=
a+bcos
-
=5,解得
a+bcos
=
∴f(-
)=
a+bcos
-
-1=
-
-1=4,
故答案为:4.
| π |
| 6 |
∴f(
| π |
| 6 |
| π2 |
| 36 |
| π |
| 6 |
| 1 |
| 2 |
| π2 |
| 36 |
| π |
| 6 |
| 11 |
| 2 |
∴f(-
| π |
| 6 |
| π2 |
| 36 |
| π |
| 6 |
| 1 |
| 2 |
| 11 |
| 2 |
| 1 |
| 2 |
故答案为:4.
点评:本题主要考查函数值的计算,利用条件直接建立方程即可,比较基础.

练习册系列答案
相关题目
已知cos(
-α)=
,则cos(
π+α)=( )
| π |
| 6 |
| 1 |
| 3 |
| 5 |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
 选修4-5不等式选讲
选修4-5不等式选讲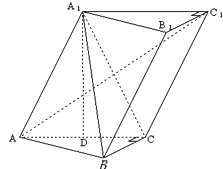 在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,A1在底面ABC上的射影恰为AC的中点D.
在三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=AA1=2,A1在底面ABC上的射影恰为AC的中点D.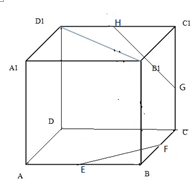 如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.
如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱AB、BC、CC1、C1D1的中点.证明:FE、HG、DC三线共点.