题目内容
 选修4-5不等式选讲
选修4-5不等式选讲设函数f(x)=|3x+6|+1
(Ⅰ)画出函数y=f(x)的图象;
(Ⅱ)若不等式,f(x)≥ax恒成立,求实数a的取值范围.
考点:函数恒成立问题,函数图象的作法
专题:函数的性质及应用
分析:(1)先去掉绝对值符号,转化为一次函数的图象画法问题;
(2)在同一坐标系中画出f(x)和y=ax的图象,利用旋转的方法得到两函数图象无交点时a的范围.
(2)在同一坐标系中画出f(x)和y=ax的图象,利用旋转的方法得到两函数图象无交点时a的范围.
解答:
解:(Ⅰ)由于f(x)=
.
则函数的图象如图所示(黑线部分):
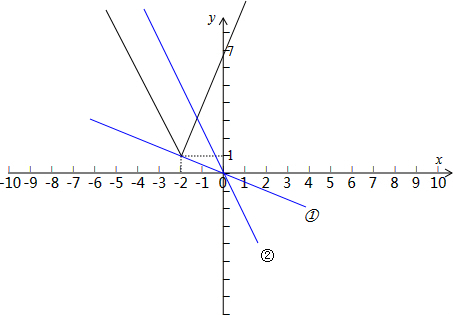
(Ⅱ) 由函数y=f(x)(黑线部分)与函数y=ax(蓝线部分)的图象(见上图)可知,
当且仅当-
≤a≤3时,即直线从图中①的位置逆时针绕原点旋转到与直线y=3x+7平行的位置时,函数y=ax的图象与函数y=f(x)图象没有交点,
所以不等式f(x)≥ax恒成立.
则a的取值范围为[-
,3].
|
则函数的图象如图所示(黑线部分):

(Ⅱ) 由函数y=f(x)(黑线部分)与函数y=ax(蓝线部分)的图象(见上图)可知,
当且仅当-
| 1 |
| 2 |
所以不等式f(x)≥ax恒成立.
则a的取值范围为[-
| 1 |
| 2 |
点评:本题考查了分段函数的图象的画法,以及利用图象解决不等式恒成立问题的思路,即作出图象,理解a的几何意义,利用旋转完成解题.

练习册系列答案
相关题目
下列不等式中:
①x2+3x-2>0和x2+3x-4>0;
②4x+
>8+
和4x>8;
③4x+
>8+
和4x>8;
④
>0和(x+3)(2-x)>0;
不等价的是( )
①x2+3x-2>0和x2+3x-4>0;
②4x+
| 5 |
| x+3 |
| 5 |
| x+3 |
③4x+
| 5 |
| x-3 |
| 5 |
| x-3 |
④
| x+3 |
| 2-x |
不等价的是( )
| A、①和② | B、①和③ |
| C、②和③ | D、②、③和④ |
下列说法中正确的是( )
| A、频率是概率的近似值,随着试验次数增加,频率会越来越接近概率 |
| B、要从1002名学生中用系统抽样的方法选取一个容量为20的样本,需要剔除2名学生,这样对被剔除者不公平 |
| C、根据样本估计总体,其误差与所选取的样本容量无关 |
| D、数据2,3,4,5的方差是数据4,6,8,10的方差的一半 |
设函数f(x)=x-
,对任意x∈[1,+∞),f(mx)+mf(x)>0恒成立,则实数m的取值范围是( )
| 1 |
| x |
| A、(-∞,-1)∪(1,+∞) |
| B、(1,+∞) |
| C、(-∞,-1) |
| D、不能确定 |